题目内容
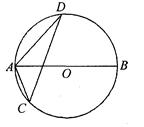
在Rt△ACB中,∠C=90°,AC=3cm,BC=4cm,以BC为直径作⊙O交AB于点D.
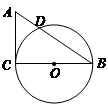
(1)求线段AD的长度;
(2)点E是线段AC上的一点,试问当点E在什么位置时,直线ED与⊙O相切?请说明理由.
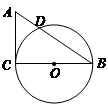
(1)求线段AD的长度;
(2)点E是线段AC上的一点,试问当点E在什么位置时,直线ED与⊙O相切?请说明理由.
(1)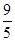 (2)在AC的中点时
(2)在AC的中点时
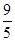 (2)在AC的中点时
(2)在AC的中点时试题分析:(1)在Rt△ACB中,∵AC=3cm,BC=4cm,∠ACB=90°,∴AB=5cm. 1分
连结CD,∵BC为直径,∴∠ADC =∠BDC =90°.
∵∠A=∠A,∠ADC=∠ACB,∴Rt△ADC∽Rt△ACB.
∴
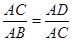 ,∴
,∴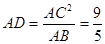 . 4分
. 4分(2)当点E是AC的中点时,ED与⊙O相切. 5分
证明:连结OD,∵DE是Rt△ADC的中线.
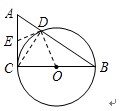
∴ED=EC,∴∠EDC=∠ECD.
∵OC=OD,∴∠ODC =∠OCD. 7分
∴∠EDO=∠EDC+∠ODC=∠ECD+∠OCD =∠ACB =90°.
∴ED与⊙O相切.
点评:本题属于对圆的切线等基本性质的熟练掌握

练习册系列答案
相关题目
 的中点,DE垂直于AC的延长线于E,连结BC,若DE=6cm,CE=2cm,下列结论错误的是( )
的中点,DE垂直于AC的延长线于E,连结BC,若DE=6cm,CE=2cm,下列结论错误的是( )
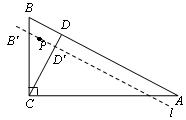
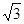 cm ,BC=6cm,经过A,B的直线l以1cm/秒的速度向下作匀速平移运动,交BC于点B′,交CD于点 D′,与此同时,点P从点B′ 出发,在直线l上以1cm/秒的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.
cm ,BC=6cm,经过A,B的直线l以1cm/秒的速度向下作匀速平移运动,交BC于点B′,交CD于点 D′,与此同时,点P从点B′ 出发,在直线l上以1cm/秒的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.