Question

【题目】如图，在正方形ABCD中，E，F是对角线B上两点，且∠EAF＝45°，将△ADF绕点A顺时针旋转90°后得到△ABQ，连接EQ，

求证：（1）EA是∠QAF的平分线；

（2）BD＝BE+QE+QB．

Answer 1

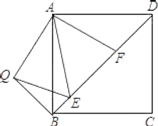
【答案】（1）见解析；（2）见解析

【解析】

（1）由旋转的性质可知∠QAF=90°，再证明∠EAF=∠EAQ=45°即可说明EA是∠QAF的平分线；

（2）先证明△QAE≌△FAE得到QE=EF，则BD=BE+EF+FD=BE+QE+QB．

解：证明：（1）由旋转的性质可知∠QAF＝90°，

∵∠EAF＝45°，

∴∠EAQ＝∠QAF﹣∠EAF＝90°﹣45°＝45°．

∴∠EAF＝∠EAQ．

∴EA是∠QAF的平分线；

（2）由旋转的性质可知AQ＝AF，QB＝FD，

由（1）可知∠EAQ＝∠EAF＝45°，

又AE＝AE，

∴△QAE≌△FAE（SAS）．

∴QE＝EF．

∴BD＝BE+EF+FD＝BE+QE+QB．