题目内容
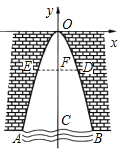
【题目】如图,一个涵洞的截面边缘是抛物线形.现测得当水面宽AB=1.6m时,涵洞顶点与水面的距离是2.4m.这时,离开水面1.5m处,涵洞的宽DE为_____.
【答案】![]()
【解析】
根据此抛物线经过原点,可设函数关系式为y=ax2.根据AB=1.6,涵洞顶点O到水面的距离为2.4m,那么B点坐标应该是(0.8,-2.4),利用待定系数法即可求出函数的解析式,继而求出点D的坐标及ED的长.
∵抛物线y=ax2(a<0),
由CO和AB的长,那么点B的坐标为(0.8,﹣2.4),
∵点B在抛物线上,将B(0.8,﹣2.4)代入y=ax2(a<0),
求得a=![]() ,
,
所求解析式为y=![]() x2.
x2.
∵![]() ,
,
∴设D点坐标为(x,﹣0.9),
则有:﹣0.9=![]() x2,
x2,
解得:x=±![]() ,
,
所以宽度为![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】某市将实行居民生活用电阶梯电价方案,如下表,图中折线反映了每户居民每月电费![]() (元)与用电量
(元)与用电量![]() (度)间的函数关系.
(度)间的函数关系.
档次 | 第一档 | 第二档 | 第三档 |
每月用电量 |
|
|
|
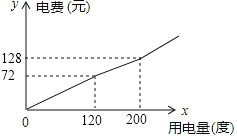
(1)小王家某月用电![]() 度,需交电费___________元;
度,需交电费___________元;
(2)求第二档电费![]() (元)与用电量
(元)与用电量![]() (度)之间的函数关系式;
(度)之间的函数关系式;
(3)小王家某月用电![]() 度,交纳电费
度,交纳电费![]() 元,请你求出第三档每度电费比第二档每度电费多多少元?
元,请你求出第三档每度电费比第二档每度电费多多少元?