题目内容
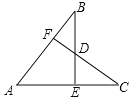
【题目】如图,四边形![]() 是菱形,
是菱形,![]() 在
在![]() 上,
上,![]() 在
在![]() 延长线上,
延长线上,![]() 和
和![]() 相交于点
相交于点![]() ,若
,若![]() ,
,![]() ,
,![]() 的长为
的长为![]() ,则菱形
,则菱形![]() 的面积为________.
的面积为________.

【答案】![]()
【解析】
作辅助线,构建全等三角形,根据中位线定理得OM=![]() CE,ON=
CE,ON=![]() DF,则OM=ON,证明△AMO≌△AHO,得OM=OH=ON,根据等边对等角和平角的定义得:∠AMO+∠ONH=180,再由平行线的性质及四边形内角和为360°得:∠DAB+∠EGF=180°,所以得∠DAB=30°,根据30°角的性质求出菱形的高PC的长,代入面积公式求出菱形ABCD的面积.
DF,则OM=ON,证明△AMO≌△AHO,得OM=OH=ON,根据等边对等角和平角的定义得:∠AMO+∠ONH=180,再由平行线的性质及四边形内角和为360°得:∠DAB+∠EGF=180°,所以得∠DAB=30°,根据30°角的性质求出菱形的高PC的长,代入面积公式求出菱形ABCD的面积.
连接AC、BD,交于点O,分别取AE、BF的中点M、N,连接OM、ON,在AB上截取AH=AM,连接OH,过C作CP⊥AF于P.
∵四边形ABCD是菱形,∴O是BD的中点,也是AC的中点,∴OM=![]() CE,ON=
CE,ON=![]() DF.
DF.
∵CE=DF,∴OM=ON.
∵AC平分∠DAB,∴∠DAC=∠BAC.
∵AO=AO,∴△AMO≌△AHO,∴OM=OH,∠AMO=∠AHO,∴OM=OH=ON,∴∠OHN=∠ONH.
∵∠AHO+∠OHN=180°,∴∠AMO+∠ONH=180.
∵OM∥EC,ON∥DF,∴∠AMO=∠AEC,∠ONH=∠GFA,∴∠AEC+∠GFA=180°,∴∠DAB+∠EGF=180°.
∵∠CGF=30°,∴∠EGF=150°,∴∠DAB=30°.
∵AD∥BC,∴∠CBF=∠DAB=30°.
∵AB=BC=6,∴CP=![]() BC=3,∴菱形ABCD的面积=ABCP=6×3=18.
BC=3,∴菱形ABCD的面积=ABCP=6×3=18.
故答案为:18.

 阅读快车系列答案
阅读快车系列答案【题目】李红在学校的研究性学习小组中负责了解初一年级200名女生掷实心球的测试成绩.她从中随机调查了若干名女生的测试成绩(单位:米),并将统计结果绘制成了如下的统计图表(内容不完整).
测试成绩 |
|
|
|
|
| 合计 |
频数 | 3 | 27 | 9 | m | 1 | n |

请你结合图表中所提供的信息,回答下列问题:
(1)表中m= ,n= ;
(2)请补全频数分布直方图;
(3)在扇形统计图中,![]() 这一组所占圆心角的度数为 度;
这一组所占圆心角的度数为 度;
(4)如果掷实心球的成绩达到6米或6米以上为优秀,请你估计该校初一年级女生掷实心球的成绩达到优秀的总人数.