题目内容
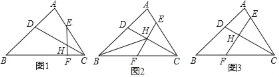
【题目】△ABC中,BC>AC,CD平分∠ACB交于AB于D,E,F分别是AC,BC边上的两点,EF交于CD于H,
(1)如图1,若∠EFC=∠A,求证:CECD=CHBC;
(2)如图2,若BH平分∠ABC,CE=CF,BF=3,AE=2,求EF的长;
(3)如图3,若CE≠CF,∠CEF=∠B,∠ACB=60°,CH=5,CE=4![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)2![]() ; (3)
; (3)![]() .
.
【解析】
(1)只要证明△ECH∽△BCD,可得![]() =
=![]() ,即可推出CECD=CHBC;
,即可推出CECD=CHBC;
(2)如图2中,连接AH.只要证明△AEH∽△HFB,可得![]() =
=![]() ,推出FH2=6,推出HE=HF=
,推出FH2=6,推出HE=HF=![]() ,即可解决问题.
,即可解决问题.
(3)只要证明△ECF∽△BCA,求出CF即可解决问题.
(1)证明:如图1中,
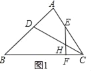
∵∠EFC+∠FEC+∠ECF=180°,∠A+∠B+∠ACB=180°,
又∵∠EFC=∠A,∠ECF=∠ACB,
∴∠CEF=∠B,∵∠ECH=∠DCB,
∴△ECH∽△BCD,
∴![]() ,
,
∴CECD=CHBC.
(2)解:如图2中,连接AH.
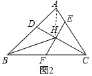
∵BH、CH都是△ABC的角平分线,
∴AH是△ABC的角平分线,
∴∠BHC=180°﹣![]() (∠ABC+∠ACB)=180°﹣
(∠ABC+∠ACB)=180°﹣![]() (180°﹣∠BAC)=90°+
(180°﹣∠BAC)=90°+![]() BAC=90°+∠HAE,
BAC=90°+∠HAE,
∵CE=CF,∠HCE=∠HCF,
∴CH⊥EF,HF=HE,
∴∠CHF=90°,
∵∠BHC=∠BHF+∠CHF=∠BHF+90°,
∴∠HAE=∠BHF,
∵∠CFE=∠CEF,
∴∠AEH=∠BFH,
∴△AEH∽△HFB,
∴![]() ,
,
∴FH2=6,
∴HE=HF=![]() ,
,
∴EF=2![]() .
.
(3)解:如图3中,作HM⊥AC于M,HN⊥BC于N.设HF=x,FN=y.
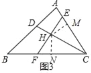
∵∠HCM=∠HCN=30°,HC=5,
∴HM=HN=![]() span>,CM=CN=
span>,CM=CN=![]() ,
,
∵CE=4![]() ,
,
∴EM=![]() ,EH=
,EH=![]() ,
,
∵S△HCF:S△HCE=FH:EH=FC:EC,
∴x:![]() =(y+
=(y+![]() ):4
):4![]() ①,
①,
又∵x2=y2+(![]() )2,
)2,
解得y=![]() 或
或![]() (舍弃),
(舍弃),
∴CF=![]() ,
,
∵∠CEF=∠B,∠ECF=∠ACB,
∴△ECF∽△BCA,
∴![]() ,
,
∴![]() =
=![]() .
.

 精英口算卡系列答案
精英口算卡系列答案