题目内容
【题目】如图,在![]() 中,
中,![]() 为锐角,点
为锐角,点![]() 为射线
为射线![]() 上一动点,连接
上一动点,连接![]() .以
.以![]() 为直角边且在
为直角边且在![]() 的上方作等腰直角三角形
的上方作等腰直角三角形![]() .
.
(1)若![]() ,
,![]()
①当点![]() 在线段
在线段![]() 上时(与点
上时(与点![]() 不重合),试探讨
不重合),试探讨![]() 与
与![]() 的数量关系和位置关系;
的数量关系和位置关系;
②当点![]() 在线段
在线段![]() 的延长线上时,①中的结论是否仍然成立,请在图2中面出相应的图形并说明理由;
的延长线上时,①中的结论是否仍然成立,请在图2中面出相应的图形并说明理由;
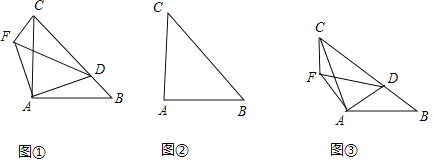
(2)如图3,若![]() ,
,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动,试探究
上运动,试探究![]() 与
与![]() 的位置关系.
的位置关系.
【答案】(1)①CF⊥BD,证明见解析;②成立,理由见解析;(2)CF⊥BD,证明见解析.
【解析】
(1)①根据同角的余角相等求出∠CAF=∠BAD,然后利用“边角边”证明△ACF和△ABD全等,②先求出∠CAF=∠BAD,然后与①的思路相同求解即可;
(2)过点A作AE⊥AC交BC于E,可得△ACE是等腰直角三角形,根据等腰直角三角形的性质可得AC=AE,∠AED=45°,再根据同角的余角相等求出∠CAF=∠EAD,然后利用“边角边”证明△ACF和△AED全等,根据全等三角形对应角相等可得∠ACF=∠AED,然后求出∠BCF=90°,从而得到CF⊥BD.
解:(1)①∵∠BAC=90°,△ADF是等腰直角三角形,
∴∠CAF+∠CAD=90°,∠BAD+∠ACD=90°,
∴∠CAF=∠BAD,
在△ACF和△ABD中,
∵AB=AC,∠CAF=∠BAD,AD=AF,
∴△ACF≌△ABD(SAS),
∴CF=BD,∠ACF=∠ABD=45°,
∵∠ACB=45°,
∴∠FCB=90°,
∴CF⊥BD;
②成立,理由如下:如图2:
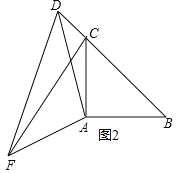
∵∠CAB=∠DAF=90°,
∴∠CAB+∠CAD=∠DAF+∠CAD,
即∠CAF=∠BAD,
在△ACF和△ABD中,
∵AB=AC,∠CAF=∠BAD,AD=AF,
∴△ACF≌△ABD(SAS),
∴CF=BD,∠ACF=∠B,
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∴∠BCF=∠ACF+∠ACB=45°+45°=90°,
∴CF⊥BD;
(2)如图3,过点A作AE⊥AC交BC于E,

∵∠BCA=45°,
∴△ACE是等腰直角三角形,
∴AC=AE,∠AED=45°,
∵∠CAF+∠CAD=90°,∠EAD+∠CAD=90°,
∴∠CAF=∠EAD,
在△ACF和△AED中,
∵AC=AE,∠CAF=∠EAD,AD=AF,
∴△ACF≌△AED(SAS),
∴∠ACF=∠AED=45°,
∴∠BCF=∠ACF+∠BCA=45°+45°=90°,
∴CF⊥BD.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某电器超市销售A B两种型号的电风扇,A型号每台进价为200元,B型号每台进价分别为150元,下表是近两天的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一天 | 3台 | 5台 | 1620元 |
第二天 | 4台 | 10台 | 2760元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润不少于1060元的目标?若能,请给出相应的采购方案;若不能,请说明理由.