题目内容
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
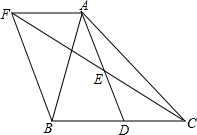
(1)试判断线段BD与CD的大小关系;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论;
(3)若△ABC为直角三角形,且∠BAC=90°时,判断四边形AFBD的形状,并说明理由.

(1)试判断线段BD与CD的大小关系;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论;
(3)若△ABC为直角三角形,且∠BAC=90°时,判断四边形AFBD的形状,并说明理由.
(1)BD=CD;(2)矩形;(3)菱形
试题分析:(1)根据平行线的性质可得∠FAE=∠CDE,再结合∠AEF=∠DEC,AE=DE,即可证得△AEF≌△DEF,从而可以证得结论;
(2)由AF∥BC,AF=BD可证得四边形AFBD是平行四边形,再根据等腰三角形的性质可得AD⊥BC,即可证得四边形AFBD是矩形;
(3)先根据直角三角形斜边的中线是斜边的一半可证得BD=AD,再结合四边形AFBD是平行四边形可证得四边形AFBD是菱形.
(1)∵AF∥BC,
∴∠FAE=∠CDE,
∵∠AEF=∠DEC,AE=DE,
∴△AEF≌△DEF,
∴AF=CD,
∵AF=BD,
∴BD=CD;
(2)∵AF∥BC,AF=BD,
∴四边形AFBD是平行四边形,
∵AB=AC,BD=CD,
∴AD⊥BC,
∴四边形AFBD是矩形;
(3)∵∠BAC=90°,BD=CD,
∴BD=AD(直角三角形斜边的中线是斜边的一半).
∵四边形AFBD是平行四边形,
∴四边形AFBD是菱形.
本题涉及了平行线的性质,全等三角形的判定和性质,平行四边形、矩形、菱形的判定和性质,特殊四边形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.
(2)由AF∥BC,AF=BD可证得四边形AFBD是平行四边形,再根据等腰三角形的性质可得AD⊥BC,即可证得四边形AFBD是矩形;
(3)先根据直角三角形斜边的中线是斜边的一半可证得BD=AD,再结合四边形AFBD是平行四边形可证得四边形AFBD是菱形.
(1)∵AF∥BC,
∴∠FAE=∠CDE,
∵∠AEF=∠DEC,AE=DE,
∴△AEF≌△DEF,
∴AF=CD,
∵AF=BD,
∴BD=CD;
(2)∵AF∥BC,AF=BD,
∴四边形AFBD是平行四边形,
∵AB=AC,BD=CD,
∴AD⊥BC,
∴四边形AFBD是矩形;
(3)∵∠BAC=90°,BD=CD,
∴BD=AD(直角三角形斜边的中线是斜边的一半).
∵四边形AFBD是平行四边形,
∴四边形AFBD是菱形.
本题涉及了平行线的性质,全等三角形的判定和性质,平行四边形、矩形、菱形的判定和性质,特殊四边形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
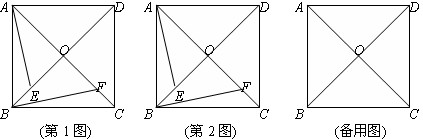
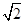 , 3
, 3