��Ŀ����
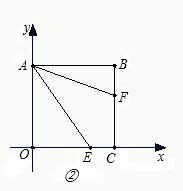
��ͼ��ƽ��ֱ������ϵ�У��ı���OABCΪ�����Σ�E����x������������˶�����F��CB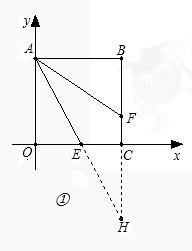 ���ϣ��ҡ�OAE=��FAE
���ϣ��ҡ�OAE=��FAE��ͼ���У�E����OC���ϣ�CE=
| 1 |
| 2 |
��1����E����OC���ϣ�CE=
| 1 |
| 3 |
��2����E����OC���ϣ�CE=
| 1 |
| n |
��3����A�������Ϊ��0��6����E����x������������˶�����F��ֱ��CB�ϣ��ҡ�OAE=��FAE����AF��CF���2����λ����ʱ���������ʱE������꣮
��������1������ӳ�AE��BC�ཻ�ڵ�H���������Ƕ�Ӧ��ȵ���������������֤��AOE�ס�HCE���ó�CH=
OA������֪������OAE=��FAE��ƽ���ߵ����ʵó���FAE=��H����AF=HF���Ӷ��ó�AF=CF+
OC��
��2������֪�����ʽ��ۣ��ó�AF=CF+
OC��
��3������E����x������������˶����ɷֵ�E��OC���ϼ���E��OC���ӳ�������������ֱ����ۣ����ÿһ������������г�����n�ķ��̣����n��ֵ�������õ�E������꣮
| 1 |
| 2 |
| 1 |
| 2 |
��2������֪�����ʽ��ۣ��ó�AF=CF+
| 1 |
| n-1 |
��3������E����x������������˶����ɷֵ�E��OC���ϼ���E��OC���ӳ�������������ֱ����ۣ����ÿһ������������г�����n�ķ��̣����n��ֵ�������õ�E������꣮
��� �⣺��1���ӳ�AE��BC�ཻ�ڵ�H��
�⣺��1���ӳ�AE��BC�ཻ�ڵ�H��
��AO��BC��
���AOC=��HCE����OAE=��CHE��
���AOE�ס�HCE��
��AO��CH=OE��CE=2��1��
��CH=
OA��
�ߡ�OAE=��CHE����OAE=��FAE��
���FAE=��H��
��AF=HF��
��HF=CF+CH��OC=OA��
��AF=CF+
OC��
��2��AF=CF+
OC
��3����E��OC����ʱ��AF=CF+
OC��
��AF-CF=
OC��
��2=
•6��
��n=4��
EΪ��4.5��0������2�֣�
��E��OC�ӳ�����ʱ��AF=CF-
OC��
��CF-AF=
OC��
��2=
•6��
��n=2��
EΪ��8��0������3�֣�
 �⣺��1���ӳ�AE��BC�ཻ�ڵ�H��
�⣺��1���ӳ�AE��BC�ཻ�ڵ�H����AO��BC��
���AOC=��HCE����OAE=��CHE��
���AOE�ס�HCE��
��AO��CH=OE��CE=2��1��
��CH=
| 1 |
| 2 |
�ߡ�OAE=��CHE����OAE=��FAE��
���FAE=��H��
��AF=HF��
��HF=CF+CH��OC=OA��
��AF=CF+
| 1 |
| 2 |
��2��AF=CF+
| 1 |
| n-1 |
��3����E��OC����ʱ��AF=CF+
| 1 |
| n-1 |
��AF-CF=
| 1 |
| n-1 |
��2=
| 1 |
| n-1 |
��n=4��
EΪ��4.5��0������2�֣�
��E��OC�ӳ�����ʱ��AF=CF-
| 1 |
| n+1 |
��CF-AF=
| 1 |
| n+1 |
��2=
| 1 |
| n+1 |
��n=2��
EΪ��8��0������3�֣�
�����������ۺϿ����������ε����ʣ�ȫ�������Ρ����������ε��ж���֪ʶ��ͬʱҲ������ѧ���ķ����������������ѶȽϴ�

��ϰ��ϵ�д�
 ������ϵ�д�
������ϵ�д� �±�Сѧ��Ԫ�Բ���ϵ�д�
�±�Сѧ��Ԫ�Բ���ϵ�д�
�����Ŀ
 ��ͼ��ƽ��ֱ������ϵ�У�OΪֱ��������ABC��ֱ�Ƕ��㣬��B=30�㣬��Ƕ���A��˫����
��ͼ��ƽ��ֱ������ϵ�У�OΪֱ��������ABC��ֱ�Ƕ��㣬��B=30�㣬��Ƕ���A��˫���� =2
=2 ��ͼ��ƽ��ֱ������ϵ�У�OB��x���ϣ���ABO=90�㣬��A������Ϊ��1��2��������AOB�Ƶ�A��ʱ����ת90�㣬���O�Ķ�Ӧ��C������Ϊ��������
��ͼ��ƽ��ֱ������ϵ�У�OB��x���ϣ���ABO=90�㣬��A������Ϊ��1��2��������AOB�Ƶ�A��ʱ����ת90�㣬���O�Ķ�Ӧ��C������Ϊ��������
 ��ͼ��ƽ��ֱ������ϵ�У�A������Ϊ��8��0����B������Ϊ��0��6��C���߶�AB���е㣮������y�����Ƿ����һ��P��ʹ����P��B��CΪ��������������AOB���ƣ������ڣ����P�����ꣻ�������ڣ�˵�����ɣ�
��ͼ��ƽ��ֱ������ϵ�У�A������Ϊ��8��0����B������Ϊ��0��6��C���߶�AB���е㣮������y�����Ƿ����һ��P��ʹ����P��B��CΪ��������������AOB���ƣ������ڣ����P�����ꣻ�������ڣ�˵�����ɣ�