题目内容
 如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线y=
如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线y=| 1 | x |
分析:题目已知条件告诉点O是一个定点,∠A、∠B是定角,定点A在移动的过程中,点B随之移动,但是△ABC的三个角的大小保持不变,∠A永远为60°,∠B永远为30°,所以点B在随点A移动的过程中所经过的路线是一条双曲线,这样就可以点A的坐标求出B点坐标,从而求出解析式.
解答: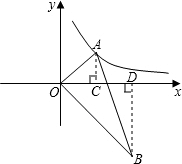 解:作AC⊥x轴于点C,BD⊥x轴于点D,
解:作AC⊥x轴于点C,BD⊥x轴于点D,
当x=1时,y=1
∴A(1,1)
∴AC=OC=1,
∴∠AOC=45°
∵∠AOB=90°
∴∠BOD=45°
由勾股定理得:AO=
在Rt△AOB中,由勾股定理得:OB=
在Rt△BOD中,由勾股定理得:DO=DB=
B(
,-
)
设点B所在的解析式为y=
∴-
=
∴k=-3
∴点B所在的解析式为y=-
.
故答案为:y=-
 解:作AC⊥x轴于点C,BD⊥x轴于点D,
解:作AC⊥x轴于点C,BD⊥x轴于点D,当x=1时,y=1
∴A(1,1)
∴AC=OC=1,
∴∠AOC=45°
∵∠AOB=90°
∴∠BOD=45°
由勾股定理得:AO=
| 2 |
在Rt△AOB中,由勾股定理得:OB=
| 6 |
在Rt△BOD中,由勾股定理得:DO=DB=
| 3 |
B(
| 3 |
| 3 |
设点B所在的解析式为y=
| k |
| x |
∴-
| 3 |
| k | ||
|
∴k=-3
∴点B所在的解析式为y=-
| 3 |
| x |
故答案为:y=-
| 3 |
| x |
点评:本题是一道反比例函数的综合试题,考查反比例函数的图象特征,等腰直角三角形的性质,直角三角形中30°所对的直角边等于斜边的一半及勾股定理的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 =2
=2 如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
 如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.
如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.