题目内容
如图:平面直角坐标系中,△ABC的三个顶点的坐标为A(a,0),B(b,0),C(0,c),且a,b,c满足
+|b-2|+(c-b)2=0.点D为线段OA上一动点,连接CD.
(1)判断△ABC的形状并说明理由;
(2)如图,过点D作CD的垂线,过点B作BC的垂线,两垂线交于点G,作GH⊥AB于H,求证:
=
;
(3)如图,若点D到CA、CO的距离相等,E为AO的中点,且EF∥CD交y轴于点F,交CA于M.求
的值.

| a+2 |
(1)判断△ABC的形状并说明理由;
(2)如图,过点D作CD的垂线,过点B作BC的垂线,两垂线交于点G,作GH⊥AB于H,求证:
| S△CAD |
| S△DGH |
| AD |
| GH |
(3)如图,若点D到CA、CO的距离相等,E为AO的中点,且EF∥CD交y轴于点F,交CA于M.求
| FC+2AE |
| 3AM |

分析:(1)根据非负数的性质建立一个方程组,求出其解就可以得出A、B、C的坐标,从而可以求出OA、OB、OC的值,由勾股定理的逆定理就可以求出△ABC的形状.
(2)由条件可以得出∠DCO=∠GDH,就有tan∠DCO=tan∠GDH,设OD=b,BH=a,则HO=2-a,根据
=
,就可以求出a、b的关系从而得出OC=DH,最后根据三角形的面积公式就可以求出结论.
(3)过点D作DG⊥AC于G,设DO=x,在Rt△AGD中由勾股定理可以得出x=2
-2,进而可以求出AD、ED的值,再由相似三角形的性质就可以得出CF、AM的值,从而可以求出
的值.
(2)由条件可以得出∠DCO=∠GDH,就有tan∠DCO=tan∠GDH,设OD=b,BH=a,则HO=2-a,根据
| b |
| 2 |
| a |
| b+2-a |
(3)过点D作DG⊥AC于G,设DO=x,在Rt△AGD中由勾股定理可以得出x=2
| 2 |
| FC+2AE |
| 3AM |
解答:解:(1)∵
+|b-2|+(c-b)2=0,
∴
,
∴
.
∵A(a,0),B(b,0),C(0,c),
∴A(-2,0),B(2,0),C(0,2),
∴AO=2,BO=2,CO=2,
∴AB=4,
∴AB2=16
在Rt△AOC和Rt△BOC中,由勾股定理可以得出
AC2=8,BC2=8,
∴AC=BC,AC2+BC2=16,
∴AB2=AC2+BC2,
∴△ABC是等腰直角三角形.
(2)∵GD⊥CD,GB⊥BC,GH⊥AB,
∴∠CDG=∠CBG=∠GHD=90°.
∴∠CDO+∠GDO=∠CDO+∠DCO=90°,
∴∠DCO=∠GDH,
∴tan∠DCO=tan∠GDH.
设OD=b,BH=a,则HO=2-a,
∵tan∠DCO=
,tan∠GDH=
.
∴
=
,
∴b2+(2-a)b-2a=0
∴(b-a)(b+2)=0,
∴b=a,b=-2
∵b>0
∴b=-2(不符合题意,舍去),
∴b=a,
∴DH=2-a+a=2,
∴DH=CO.
∵S△CAD=
,S△GHD=
,
∴
=
,
∴
=
,
∵DH=CO,
∴
=
;
(3)如图2,过点D作DG⊥AC于G,
∴∠AGD=90°,
∵△ABC是等腰直角三角形,
∴∠GAD=45°,
∴∠ADG=45°,
∴∠GAD=∠ADG,
∴AG=GD.
∵DG=DO,
∴OD=GD=AG.
设DO=x,AD=2-x,在Rt△AGD中,由勾股定理,得
AD2=AG2+GD2,
(2-x)2=x2+x2,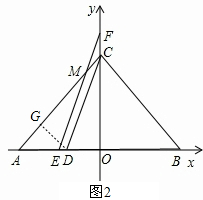
x=2
-2.
∴DO=2
-2
∵E为AO的中点,
∴AE=EO=1,
∴ED=3-2
,AD=4-2
.
∵DC∥EF,
∴
=
,
=
,
∴
=
,
=
,
∴FC=
-1,AM=
+1,
∴
=
=
.
答:
的值是
.
| a+2 |
∴
|
∴
|
∵A(a,0),B(b,0),C(0,c),
∴A(-2,0),B(2,0),C(0,2),
∴AO=2,BO=2,CO=2,
∴AB=4,
∴AB2=16
在Rt△AOC和Rt△BOC中,由勾股定理可以得出
AC2=8,BC2=8,
∴AC=BC,AC2+BC2=16,
∴AB2=AC2+BC2,
∴△ABC是等腰直角三角形.
(2)∵GD⊥CD,GB⊥BC,GH⊥AB,
∴∠CDG=∠CBG=∠GHD=90°.
∴∠CDO+∠GDO=∠CDO+∠DCO=90°,
∴∠DCO=∠GDH,
∴tan∠DCO=tan∠GDH.
设OD=b,BH=a,则HO=2-a,
∵tan∠DCO=
| b |
| 2 |
| a |
| b+2-a |
∴
| b |
| 2 |
| a |
| b+2-a |
∴b2+(2-a)b-2a=0
∴(b-a)(b+2)=0,
∴b=a,b=-2
∵b>0
∴b=-2(不符合题意,舍去),
∴b=a,
∴DH=2-a+a=2,
∴DH=CO.
∵S△CAD=
| AD•CO |
| 2 |
| DH•GH |
| 2 |
∴
| S△CAD |
| S△DGH |
| ||
|
∴
| S△CAD |
| S△DGH |
| AD•CO |
| DH•GH |
∵DH=CO,
∴
| S△CAD |
| S△DGH |
| AD |
| GH |
(3)如图2,过点D作DG⊥AC于G,
∴∠AGD=90°,
∵△ABC是等腰直角三角形,
∴∠GAD=45°,
∴∠ADG=45°,
∴∠GAD=∠ADG,
∴AG=GD.
∵DG=DO,
∴OD=GD=AG.
设DO=x,AD=2-x,在Rt△AGD中,由勾股定理,得
AD2=AG2+GD2,
(2-x)2=x2+x2,

x=2
| 2 |
∴DO=2
| 2 |
∵E为AO的中点,
∴AE=EO=1,
∴ED=3-2
| 2 |
| 2 |
∵DC∥EF,
∴
| DO |
| ED |
| CO |
| CF |
| AE |
| AD |
| AM |
| AC |
∴
2
| ||
3-2
|
| 2 |
| CF |
| 1 | ||
4-2
|
| AM | ||
2
|
∴FC=
| 2 |
| 2 |
∴
| FC+2AE |
| 3AM |
| ||
3(
|
| 1 |
| 3 |
答:
| FC+2AE |
| 3AM |
| 1 |
| 3 |
点评:本题考查了非负数的性质的运用,等腰直角三角形的判定及性质的运用,勾股定理的运用,全等三角形的判定及性质的运用,正切值的判定及运用,平行线分线段成比例定理的运用,解答本题时注意三个问题是递进关系,必须逐一解决,利用全等三角形的性质是解答第二问的关键,利用平行线分线段成比例定理是求出线段长短的关键.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
 如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线
如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线 =2
=2 如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( ) 如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.
如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.