题目内容
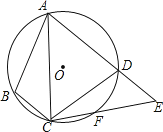
【题目】已知：如图，在菱形ABCD中，点E、F分别为边CD、AD的中点，连接AE，CF，求证：△ADE≌△CDF．
【答案】证明：∵四边形ABCD是菱形，
∴AD=CD，
∵点E、F分别为边CD、AD的中点，
∴AD=2DF，CD=2DE，
∴DE=DF，
在△ADE和△CDF中，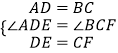 
，
∴△ADE≌△CDF（SAS）．
【解析】由菱形的性质得出AD=CD，由中点的定义证出DE=DF，由SAS证明△ADE≌△CDF即可．此题主要考查了全等三角形的判定、菱形的性质；熟练掌握菱形的性质，证明三角形全等是解决问题的关键．
【考点精析】根据题目的已知条件，利用菱形的性质的相关知识可以得到问题的答案，需要掌握菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半．
练习册系列答案
相关题目
【题目】我们在学完“平移、轴对称、旋转”三种图形的变化后，可以进行进一步研究，请根据示例图形，完成下表．
图形的变化 | 示例图形 | 与对应线段有关的结论 | 与对应点有关的结论 |
平移 |
| AA′=BB′ | |
轴对称 |
| ||
旋转 |
| AB=A′B′；对应线段AB和A′B′所在的直线相交所成的角与旋转角相等或互补． |
