题目内容
【题目】如图,正八边形各边中点构成四边形,则正八边形边长与AB的比是( )
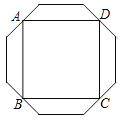
A. 2﹣![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
过E作EF⊥AD于F,过G作GH⊥AD于H,于是得到△AEF与△DGH是等腰直角三角形,四边形EFHG是矩形,根据等腰直角三角形和矩形的性质得到AF=EF=DH=GH,EG=FH,设AF=EF=GH=DH=k,得到EG=2AE=2![]() k,AB=AD=2
k,AB=AD=2![]() k+2k,于是得到结论.
k+2k,于是得到结论.
过E作EF⊥AD于F,过G作GH⊥AD于H,
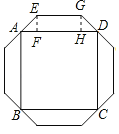
则△AEF与△DGH是等腰直角三角形,四边形EFHG是矩形,
∴AF=EF=DH=GH,EG=FH,
设AF=EF=GH=DH=k,
∴AE=DG=![]() k,
k,
∴EG=2AE=2![]() k,
k,
∴AB=AD=2![]() k+2k,
k+2k,
∴正八边形边长与AB的比=![]() ,
,
故选A.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目