题目内容
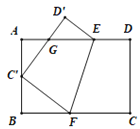
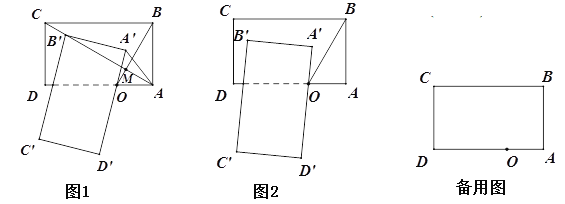
【题目】如图:已知矩形ABCD中,AB=![]() cm,BC=3cm,点O在边AD上,且AO=1cm.将矩形ABCD绕点O逆时针旋转
cm,BC=3cm,点O在边AD上,且AO=1cm.将矩形ABCD绕点O逆时针旋转![]() 角(
角(![]() ),得到矩形A′B′C′D′
),得到矩形A′B′C′D′
(1)求证:AC⊥OB;
(2)如图1, 当B′落在AC上时,求AA′;
(3)如图2,求旋转过程中△CC′D′的面积的最大值.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由三角函数可求得∠AOB=60°,∠CAD=30°,易证AC⊥OB;
(2)求出OB、BB′,利用![]() 可求得
可求得![]() ;
;
(3)过C点作CH⊥于C′D′点H,连结OC,则CH≤OC+OD′,由此可判断出D′在CO的延长线上时△CC′D′的面积最大,然后根据三角形面积公式求解即可.
解:(1)Rt△OAB中,![]() ∴∠AOB=60°
∴∠AOB=60°
Rt△ACD中,![]()
∴∠CAD=30°
∴∠OMA=180°-60°-30°=90°
即AC⊥OB
(2)Rt△OAM中,![]()
Rt△OAB中,OB′=OB=![]() =2,
=2,
Rt△O B′M中,B′M=![]() ,
,
BM=OB-OM=![]() ,
,
Rt△BB′M中,![]()
![]()
∴![]() ,
,
∴![]()
(3)如图,过C点作CH⊥于C′D′点H,连结OC,则CH≤OC+OD′
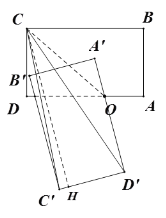
只有当D′在CO的延长线上时,CH才最大.
又C′D′长一定,故此时△CC′D′的面积的最大.
而![]()
∴△CC′D′的最大面积为![]()

练习册系列答案
相关题目