题目内容
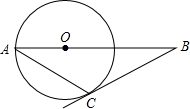
如图，AB是⊙O的直径，C为AB延长线上一点，CD与⊙O相切，切点为E，AD⊥CD于点D，交⊙O于点F，若⊙O的半径为2，设BC=x，DF=y，则y关于x的函数解析式为y=______．
连接OE，BF，
∵CD与圆O相切，∴OE⊥CD，
∴∠OEC=90°，又AD⊥DC，
∴∠D=∠OEC=90°，由∠C为公共角，
∴△COE∽△CAD，
∴
=
，即
=
，
∴AD=
，
又∵AB为圆O的直径，∴∠AFB=90°，
∴∠AFB=∠OEC=∠D=90°，∴BF∥CD，
∴∠ABF=∠C，
∴△ABF∽△OCE，
∴
=
，即
=
，
∴AF=
，
∴y=DF=AD-AF=
-
=
．
∵CD与圆O相切，∴OE⊥CD，
∴∠OEC=90°，又AD⊥DC，
∴∠D=∠OEC=90°，由∠C为公共角，
∴△COE∽△CAD，
∴
| OE |
| AD |
| CO |
| CA |
| 2 |
| AD |
| x+2 |
| x+4 |
∴AD=
| 2x+8 |
| x+2 |
又∵AB为圆O的直径，∴∠AFB=90°，
∴∠AFB=∠OEC=∠D=90°，∴BF∥CD，
∴∠ABF=∠C，
∴△ABF∽△OCE，
∴
| AF |
| OE |
| AB |
| OC |
| AF |
| 2 |
| 4 |
| x+2 |
∴AF=
| 8 |
| x+2 |
∴y=DF=AD-AF=
| 2x+8 |
| x+2 |
| 8 |
| x+2 |
| 2x |
| x+2 |
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
