题目内容
【题目】如图,已知△ABC是等边三角形.
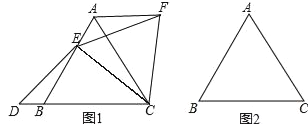
(1)如图(1),点E在线段AB上,点D在射线CB上,且ED=EC.将△BCE绕点C顺时针旋转60°至△ACF,连接EF.猜想线段AB,DB,AF之间的数量关系;
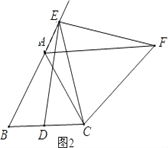
(2)点E在线段BA的延长线上,其它条件与(1)中一致,请在图(2)的基础上将图形补充完整,并猜想线段AB,DB,AF之间的数量关系;
(3)请选择(1)或(2)中的一个猜想进行证明.
【答案】(1)猜想:AB=AF+BD;(2)猜想:AB=AF﹣BD;(3)AB=AF+BD.证明见解析.
【解析】整体分析:
(1)由于AF=BE,可能有BD=AE,因此猜想AB=AF+BD;(2)根据题意,画出图形,由图形猜想AB=AF﹣BD;(3)证猜想(1),过点E作EG∥BC交AC于点G,则△AEG为等边三角形,可证△BDE≌△GEC,得BD=AE,即可证明.
解:(1)猜想:AB=AF+BD;
(2)如图2,猜想:AB=AF﹣BD;
(3)如图(1),过点E作EG∥BC交AC于点G,得△AEG为等边三角形,

∵DE=CE,
∴∠CDE=∠ECD,
又∵∠CDE+∠BED=∠ABC=∠ACD=∠ECD+∠GCE,
∴∠BED=∠GCE,
在△BDE和△GEC中,
 ,
,
∴△BDE≌△GEC,
∴BD=EG=AE
又∵AF=BE,
∴AB=BE+AE=AF+BD.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目