ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌABЃНACЃН4cmЃЌЁЯBACЃН90ЁуЃЎЖЏЕуPЁЂQЭЌЪБДгAЁЂBСНЕуГіЗЂЃЌЗжБ№биABЁЂBCЗНЯђдШЫйвЦЖЏЃЌЫќУЧЕФЫйЖШЖМЪЧ1cm/sЃЌЕБЕуPЕНДяЕуBЪБЃЌPЁЂQСНЕуЭЃжЙдЫЖЏЃЎЩшЕуPЕФдЫЖЏЪБМфЮЊtsЃЌЫФБпаЮAPQCЕФУцЛ§ЮЊycm2 ЃЎ
(1)ЕБtЮЊКЮжЕЪБЃЌЁїPBQЪЧжБНЧШ§НЧаЮ?
(2)ЂйЧѓyгыtЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіtЕФШЁжЕЗЖЮЇЃЛ
ЂкЕБtЮЊКЮжЕЪБЃЌyШЁЕУзюаЁжЕЃПзюаЁжЕЮЊЖрЩйЃП
(3)ЩшPQЕФГЄЮЊxcmЃЌЪдЧѓyгыxЕФКЏЪ§ЙиЯЕЪНЃЎ
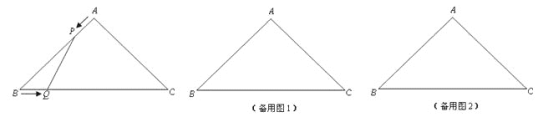
ЁОД№АИЁПЃЈ1ЃЉЕБtЃН![]() Лђ
Лђ![]() ЪБЃЌЁїPBQЪЧжБНЧШ§НЧаЮЃЛЃЈ2ЃЉЂйyЃН8Ѓ
ЪБЃЌЁїPBQЪЧжБНЧШ§НЧаЮЃЛЃЈ2ЃЉЂйyЃН8Ѓ![]() ЃЈ0ЁмtЁм4ЃЉЃЌЂкЕБtЃН2ЪБЃЌyШЁЕУзюаЁжЕЃЌзюаЁжЕЪЧ
ЃЈ0ЁмtЁм4ЃЉЃЌЂкЕБtЃН2ЪБЃЌyШЁЕУзюаЁжЕЃЌзюаЁжЕЪЧ![]() ЃЛЃЈ3ЃЉy
ЃЛЃЈ3ЃЉy![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉЗжЁЯPQBЃН90ЁуКЭЁЯQPBЃН90ЁуСНжжЧщПіЬжТлМДПЩЃЛ
ЃЈ2ЃЉИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНСаЪНyЃНSЁїABCЃSЁїBPQМДЕУКЏЪ§ЙиЯЕЪНЃЌИљОнЖўДЮКЏЪ§зюжЕдРэМДПЩЕУГіyШЁЕУзюаЁжЕЪБtЕФжЕКЭyЕФзюаЁжЕЃЛ
ЃЈ3ЃЉАбt2Ѓ4 tЃН![]() ДњШыyЃН8Ѓ
ДњШыyЃН8Ѓ![]() ЛЏМђМДПЩ.
ЛЏМђМДПЩ.
ЪдЬтНтЮіЃКЃЈ1ЃЉЕБtЃН![]() Лђ
Лђ![]() ЪБЃЌЁїPBQЪЧжБНЧШ§НЧаЮЃЌРэгЩШчЯТЃК
ЪБЃЌЁїPBQЪЧжБНЧШ§НЧаЮЃЌРэгЩШчЯТЃК
ЁпBQЃНAPЃНtЃЌ BPЃН4ЃtЃЌ
ЁрЂйЕБЁЯPQBЃН90ЁуЪБЃЌгЩ![]() ЕУЃК
ЕУЃК![]() t ЃН4ЃtЃЌНтЕУЃКtЃН
t ЃН4ЃtЃЌНтЕУЃКtЃН![]() ЃЛ
ЃЛ
ЂкЕБЁЯQPBЃН90ЁуЪБЃЌгЩ![]() ЕУЃК
ЕУЃК![]() ЃЌНтЕУЃКtЃН
ЃЌНтЕУЃКtЃН![]() .
.
ЁрЕБtЃН![]() Лђ
Лђ![]() ЪБЃЌЁїPBQЪЧжБНЧШ§НЧаЮ.
ЪБЃЌЁїPBQЪЧжБНЧШ§НЧаЮ.
ЃЈ2ЃЉЂйЙ§PзїPHЁЭBCЃЌдкRtЁїPHBжаЃЌBPЃН4ЃtЃЌPHЃН![]() ЃЌ
ЃЌ
ЁрSЁїBPQЃН![]() ЃЌ
ЃЌ
ЁрyЃНSЁїABCЃSЁїBPQЃН8Ѓ![]() .
.
гЩЬтвтПЩжЊЃК0ЁмtЁм4.
ЂкyЃН8Ѓ![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрЕБtЃН2ЪБЃЌyШЁЕУзюаЁжЕЃЌзюаЁжЕЪЧ![]() ЃЎ
ЃЎ
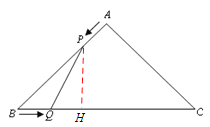
ЃЈ3ЃЉдкRtЁїPQHжаЃЌPHЃН![]() ЃЈ4ЃtЃЉЃЌHQЃН
ЃЈ4ЃtЃЉЃЌHQЃН![]() ЃЈ4ЃtЃЉЃtЃЌ
ЃЈ4ЃtЃЉЃtЃЌ
гЩPQ2ЃН PH2ЃЋHQ2ЃЌдђx2ЃНЁВ![]() ЃЈ4ЃtЃЉЁГ2ЃЋЁВ
ЃЈ4ЃtЃЉЁГ2ЃЋЁВ![]() ЃЈ4ЃtЃЉЃtЁГ2
ЃЈ4ЃtЃЉЃtЁГ2
ЛЏМђЕУЃКx2ЃНЃЈ2ЃЋ![]() ЃЉt 2Ѓ4ЃЈ2ЃЋ
ЃЉt 2Ѓ4ЃЈ2ЃЋ![]() ЃЉtЃЋ16ЃЌЁр t2Ѓ4 tЃН
ЃЉtЃЋ16ЃЌЁр t2Ѓ4 tЃН![]() .
.
НЋt2Ѓ4tЃН![]() ДњШыyЃН8Ѓ
ДњШыyЃН8Ѓ![]() ЃЌЕУyЃН8ЃЋ
ЃЌЕУyЃН8ЃЋ![]() ЁЄ
ЁЄ ЃЎ
ЃЎ

 НзЬнМЦЫуЯЕСаД№АИ
НзЬнМЦЫуЯЕСаД№АИ