Question

【题目】一个直角三角形斜边长为，内切圆半径为，则这个三角形周长是（ ）

A. B. C. D.

Answer 1

【答案】B

【解析】

设圆O的半径是r，连接OD，OE，推出正方形DCEO，得出OD=OE=CD=CE，根据切线长定理求出AF=AD，BE=BF，CE=CD，根据AC-r+BC-r=AB求出AC+BC即可．

设圆O的半径是r，连接OD，OE.

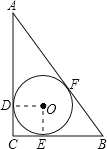
∵圆O与边AC、BC、AB分别切于点D. E.F，

∴OD⊥AC，OE⊥BC，AF=AD，BE=BF，CE=CD，

∵

∴四边形ODCE是正方形，

∴OD=OE=CD=CE，

∴AF=AD=ACr，BF=BE=BCr，

∵AB=AF+BF=(ACr)+(BCr)，

∴ACr+BCr=AB=10cm，

∴AC+BC=12cm，

∴△ABC的周长是：AC+BC+AB=22cm.

故选：B.