题目内容
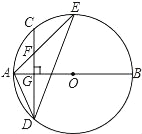
【题目】如图,在菱形ABCD中,∠BAD=120°,E为AB边上一点,过E作EG⊥BC于点G,交对角线BD于点F.
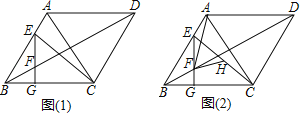
(1)如图(1),若∠ACE=15°,BC=6,求EF的长;
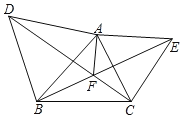
(2)如图(2),H为CE的中点,连接AF,FH,求证:AF=2FH.
【答案】(1)EF=4﹣![]() ;(2)见解析
;(2)见解析
【解析】
(1)首先证明EG=CG,设BG=x,则EG=CG=![]() x,根据BC=4,构建方程求出x,证明EF=BF,求出BF即可解决问题.
x,根据BC=4,构建方程求出x,证明EF=BF,求出BF即可解决问题.
(2)如图2,作CM⊥BC交FH的延长线于M,连接AM,AH.利用全等三角形的性质证明△FAM是等边三角形即可解决问题.
解:(1)如图1中,
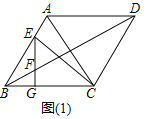
∵四边形ABCD是菱形,
∵AB=BC=CD=AD=6,AD∥BC,
∴∠ABC=180°﹣∠BAD=60°,
∴△ABC是等边三角形,
∴∠ACB=60°,
∵∠ACE=15°,
∴∠ECG=∠ACB﹣∠ACE=45°,
∵EG⊥CG,
∴∠EGC=90°,
∴EG=CG,
设BG=x,则EG=CG=![]() x,
x,
∴x+![]() x=4,
x=4,
∴x=2![]() ﹣2,
﹣2,
∵四边形ABCD是菱形,
∴∠FBG=∠EBF=30°,
∵∠BEG=30°,
∴FB=FE,
∵BF=![]() =
=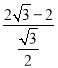 =4﹣
=4﹣![]() ,
,
∴EF=4﹣![]() .
.
(2)如图2,作CM⊥BC交FH的延长线于M,连接AM,AH.

∵EG⊥BC,MC⊥BC,
∴EF∥CM,
∴∠FEH=∠HCM,
∵∠EHF=∠CHM,EH=CH,
∴△EFH≌△CMH(ASA),
∴EF=CM,FH=HM,
∵EF=BF,
∴BF=CM,
∵∠ABF=∠ACM=30°,BA=CA,
∴△BAF≌△CAM(SAS),
∴AF=AM,∠BAF=∠CAM,
∴∠FAM=∠BAC=60°,
∴△FAM是等边三角形,
∵FH=HM,
∴AH⊥FM,∠FAH=![]() ∠FAM=
∠FAM=![]() ×60°=30°,
×60°=30°,
∴AF=2FH.

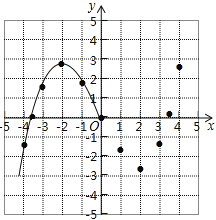
【题目】某学习小组在研究函数y=![]() x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x | … | ﹣4 | ﹣3.5 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 3.5 | 4 | … |
y | … | ﹣ | ﹣ |
|
|
| 0 | ﹣ | ﹣ | ﹣ |
|
| … |
(1)请补全函数图象;
(2)方程![]() x3﹣2x=﹣2实数根的个数为 ;
x3﹣2x=﹣2实数根的个数为 ;
(3)观察图象,写出该函数的两条性质.