题目内容
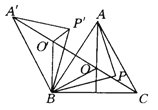
【题目】如图所示,O是锐角三角形ABC内一点,∠AOB=∠BOC=∠COA=120°,P是△ABC内不同于O的另一点,△A′BO′、△A′BP′分别由△AOB、△APB旋转而得,旋转角都为60°,则下列结论中正确的有( ).(提示:有一个角是60°的等腰三角形是等边三角形)
①△O′BO为等边三角形,且A′、O′、O、C在一条直线上.
②A′O′+O′O=AO+BO. ③A′P′+P′P=PA+PB.
④PA+PB+PC>AO+BO+CO.
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】解:连PP′,如图,∵△A′BO′,△A′BP′分别由△AOB,△APB旋转而得,旋转角都为60°,∴BO′=BO,BP′=BP,∠OBO′=∠PBP′=60°,∠A′O′B=∠AOB,O′A′=OA,P′A′=PA,∴△BOO′和△BPP′都是等边三角形,∴∠BOO′=∠BO′O=60°,OO′=OB,而∠AOB=∠BOC=∠COA=120°,∴∠A′O′O=∠O′OC=180°,即△O′BO为等边三角形,且A′,O′,O,C在一条直线上,所以①正确;
∴A′O′+O′O=AO+BO,所以②正确;
A′P′+P′P=PA+PB,所以③正确;
又∵CP+PP′+P′A′>CA′=CO+OO′+O′A′,∴PA+PB+PC>AO+BO+CO,所以④正确.
故选D.


练习册系列答案
相关题目