题目内容
【题目】如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF. 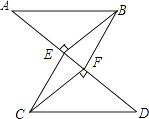
求证:
(1)BE=CF;
(2)四边形BECF是平行四边形.
【答案】
(1)证明:∵BE⊥AD,CF⊥AD,
∴∠AEB=∠DFC=90°,
∵AB∥CD,
∴∠A=∠D,
在△AEB与△DFC中,
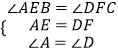 ,
,
∴△AEB≌△DFC(ASA),
∴BE=CF
(2)证明:∵BE⊥AD,CF⊥AD,
∴BE∥CF,
∵BE=CF,
∴四边形BECF是平行四边形
【解析】(1)通过全等三角形(△AEB≌△DFC)的对应边相等证得BE=CF;(2)由“在同一平面内,同垂直于同一条直线的两条直线相互平行”证得BE∥CF.易得四边形BECF是平行四边形.
【考点精析】本题主要考查了平行四边形的判定的相关知识点,需要掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形才能正确解答此题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目