Question

【题目】(2016四川省乐山市第21题)某班开展安全知识竞赛活动，班长将所有同学的成绩分成四类，并制作了如下的统计图表：

根据图表信息，回答下列问题：

（1）该班共有学生 人；表中a= ；

（2）将丁类的五名学生分别记为A、B、C、D、E，现从中随机挑选两名学生参加学校的决赛，请借助树状图、列表或其他方式求B一定能参加决赛的概率．

Answer 1

【答案】（1）40，20；（2）．

【解析】

试题分析：（1）根据丙的人数除以占的百分比求出学生总数，进而求出a的值即可；

（2）列表得出所有等可能的情况数，找出B一定参加的情况数，即可求出所求的概率．

试题解析：（1）根据题意得：10÷25%=40（人），a=40﹣5﹣10﹣5=20；故答案为：40，20；

（2）列表如下：

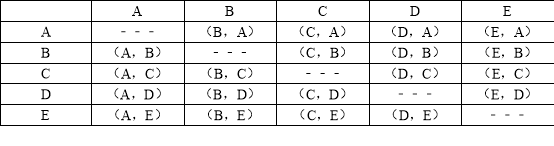
所有等可能的情况有20种，其中B一定参加的情况有8种，则P（B一定参加）==．