题目内容
【题目】(2016山东省泰安市第18题)如图，在△PAB中，PA=PB，M，N，K分别是PA，PB，AB上的点，且AM=BK，BN=AK，若∠MKN=44°，则∠P的度数为（ ）
A．44° B．66° C．88° D．92°
【答案】D
【解析】
试题分析：根据等腰三角形的性质得到∠A=∠B，证明△AMK≌△BKN，得到∠AMK=∠BKN，根据三角形的外角的性质求出∠A=∠MKN=44°，根据三角形内角和定理计算即可．∵PA=PB，∴∠A=∠B，
在△AMK和△BKN中，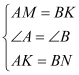
，∴△AMK≌△BKN，∴∠AMK=∠BKN，
∵∠MKB=∠MKN+∠NKB=∠A+∠AMK，∴∠A=∠MKN=44°，∴∠P=180°﹣∠A﹣∠B=92°，
练习册系列答案
相关题目
