题目内容
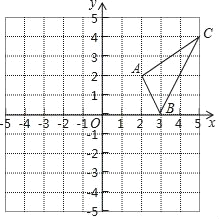
【题目】如图1,在平面直角坐标系中,O为坐标原点,抛物线y=a(x﹣h)2﹣4(a>0)与x轴分别交于原点O、A两点,点A在x轴的正半轴上,顶点为D,直线y= ![]() x交抛物线于B点,过B作BE∥x轴交抛物线另一点E,交对称轴于F.
x交抛物线于B点,过B作BE∥x轴交抛物线另一点E,交对称轴于F.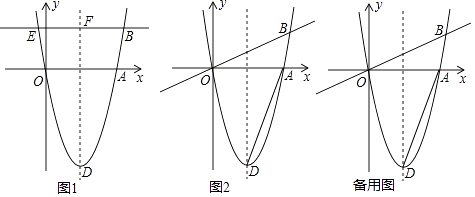
(1)当DF=4a时,求BE的长.
(2)如图2,连AD,连接AD绕点A旋转交直线OB于点G,点D的对应点为G,当OG=2时,求a的值;
(3)在(2)的条件下,当0<a<1时,以OB为直径作圆交x轴下方抛物线于点P,求点P坐标.
【答案】
(1)解:如图1中,
由题意D(h,﹣4),
∵DF=4a,
∴点F坐标(h,4a﹣4),
当y=4a﹣4时,4a﹣4=a(x﹣h)2﹣4,
解得x=h±2,
∴B(2+h,4a﹣4),E(h﹣2,4a﹣4),
∴BE=(2+h)﹣(h﹣2)=4.
(2)解:如图2中,由题意OG=2,可得G(﹣ ![]() ,﹣1)或G′(
,﹣1)或G′( ![]() ,1).
,1).

当AD=AG,A(2h,0),D(h,﹣4),
∴(2h+ ![]() )2+1=h2+16,
)2+1=h2+16,
∴h= ![]() 或﹣2
或﹣2 ![]() (舍弃),
(舍弃),
∴A( ![]() ,0),代入y=a(x﹣h)2﹣4,解得a=3,
,0),代入y=a(x﹣h)2﹣4,解得a=3,
当AD=AG′时,(2h﹣ ![]() )2+1=h2+16,
)2+1=h2+16,
解得h=2 ![]() 或﹣
或﹣ ![]() (舍弃),
(舍弃),
∴A(4 ![]() ,0),代入y=a(x﹣h)2﹣4,解得a=
,0),代入y=a(x﹣h)2﹣4,解得a= ![]() ,
,
综上所述,A的值为3或 ![]() .
.
(3)解:由题意抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() x,
x,
由  ,解得
,解得 ![]() ,或
,或 ![]() ,
,
∴B(5 ![]() ,5),
,5),
∴OB=10,
∴线段OB的中点O′( ![]() ,
, ![]() )
)
设P(m, ![]() m2﹣
m2﹣ ![]() m),
m),
由题意PO′=5,
∴(m﹣ ![]() )2+(
)2+( ![]() m2﹣
m2﹣ ![]() m﹣
m﹣ ![]() )2=52,
)2=52,
∴m2﹣5 ![]() m+
m+ ![]() +(
+( ![]() m2﹣
m2﹣ ![]() m)2﹣5(
m)2﹣5( ![]() m2﹣
m2﹣ ![]() m)+
m)+ ![]() =25,
=25,
∴m2﹣5 ![]() m+(
m+( ![]() m2﹣
m2﹣ ![]() m)(
m)( ![]() m2﹣
m2﹣ ![]() m﹣5)=0,
m﹣5)=0,
∴m2﹣5 ![]() m+
m+ ![]() m(m﹣4
m(m﹣4 ![]() )(m﹣5
)(m﹣5 ![]() )(m+
)(m+ ![]() )=0
)=0
∴ ![]() m(m﹣5
m(m﹣5 ![]() )(m2﹣3
)(m2﹣3 ![]() m﹣3)=0
m﹣3)=0
∴m=0或5 ![]() 或
或 ![]() 或
或 ![]() ,
,
∵点P在x轴下方,
∴P( ![]() ,
, ![]() ).
).
【解析】(1)由顶点式求出D(h,-4),再表示出B纵坐标,y=4a﹣4代入解析式,求出B、E两点的横坐标,求出其差,就是BE;(2)AD绕点A旋转交直线OB于点G,位置有两个,分类讨论,利用两点间距离公式列出方程,求出a值;(3)求出OB的中点,就是圆心,利用“圆上任意点到圆心距离等于半径”及两点间距离公式,列出方程,求出P的横坐标m.

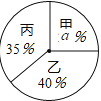
【题目】某校学生会决定从三名学生会干事中选拔一名干事,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 75 | 80 | 90 |
面试 | 93 | 70 | 68 |
根据录用程序,学校组织200名学生采用投票推荐的方式,对三人进行民主测评,三人得票率(没有弃权,每位同学只能推荐1人)如扇形统计图所示,每得一票记1分.
(1)扇形统计图中![]() = , 分别计算三人民主评议的得分;
= , 分别计算三人民主评议的得分;
(2)根据实际需要,学校将笔试、面试、民主评议三项得分按4:3:3的比例确定个人成绩,得分最高者将被选中,通过计算说明三人中谁被选中?