Question

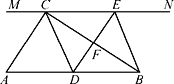
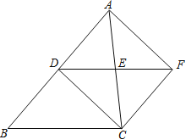
【题目】如图，在△ABC中，点D、E分别是边AB、AC的中点，将△ADE绕点E旋转180°得到△CFE．

（1）求证：四边形ADCF是平行四边形．

（2）当△ABC满足什么条件时，四边形ADCF是正方形？请说明理由．

Answer 1

【答案】（1）证明见解析（2）当∠ACB=90°，AC=BC时，四边形ADCF是正方形

【解析】

(1)利用旋转的性质得出点A、E、C三点共线,点D、E、F三点共线,且AE＝CE,DE＝FE,即可得出答案;
(2)首先得出CD⊥AB，即∠ADC＝90°,由(1)知,四边形ADCF是平行四边形,故四边形ADCF是矩形.进而求出CD＝AD即可得出答案.

（1）证明：∵△CFE是由△ADE绕点E旋转180°得到，

∴点A、E、C三点共线，点D、E、F三点共线，

且AE＝CE，DE＝FE，

故四边形ADCF是平行四边形．

（2）当∠ACB＝90°，AC＝BC时，四边形ADCF是正方形．

理由如下：在△ABC中，∵AC＝BC，AD＝BD，

∴CD⊥AB，即∠ADC＝90°．

而由（1）知，四边形ADCF是平行四边形，

∴四边形ADCF是矩形．

又∵∠ACB＝90°，

∴，

故四边形ADCF是正方形．