Question

【题目】小明同学在研究如何在△ABC内做一个面积最大的正方形时，想到了可以利用位似知识解决这个问题，他的做法是：（如图1）先在△ABC内作一个小正方形DEFG，使得顶点D落在边AB上，顶点E、F落在边BC上，然后连接BG并延长交AC边于点H，作HK⊥BC，HI∥BC，再作IJ⊥BC于J，则正方形HIJK就是所作的面积最大的正方形．

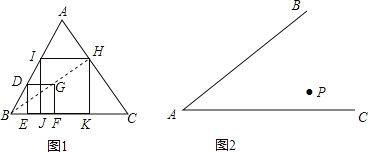
（1）若△ABC中，AB＝4，∠ABC＝60°，∠ACB＝45°，请求出小明所作的面积最大的正方形的边长．

（2）拓展运用：

如图2，已知∠BAC，在角的内部有一点P，请画一个⊙M，使得⊙M经过点P，且与AB、AC都相切．（注：并简要说明画法）

Answer 1

【答案】（1）小明所作的面积最大的正方形的边长为；（2）如图2所示，见解析.

【解析】

（1）如图1中，作AM⊥BC于M，交IH于N，设正方形边长为x，由IH∥BC，得，据此列出方程即可解决问题．
（2）作∠BAC的平分线AQ，在AQ上取一点O，作⊙O和AB、AC相切，连接AP交⊙O于E、F，然后利用位似知识，找到圆心M即可解决问题．

（1）如图1中，作AM⊥BC于M，交IH于N，设正方形边长为x．

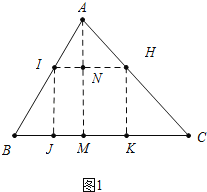
在Rt△ABM中，∵∠AMB＝90°，∠B＝60°，AB＝4，

∴BM＝2，AM＝，

∵∠C＝∠MAC＝45°，

∴AM＝MC＝，

∴BC＝2+

∵IH∥BC，

∴，

∴，

解得：x＝，

∴小明所作的面积最大的正方形的边长为；

（2）如图2中，

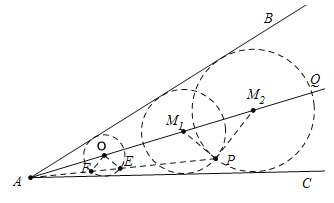
①作∠BAC的平分线AQ，

②在AQ上取一点O，作⊙O和AB、AC相切，

③连接AP交⊙O于E、F．

④作PM1∥OE交AQ于M1，

⑤以M1为圆心PM1为半径作⊙M1，

⊙M1即为所求；

同法，作PM2∥OF，交AQ于M2，

⊙M2即为所求．