题目内容
【题目】如图,在平面直角坐标系中有一个3×3的正方形网格,其右下角格点(小正方形的顶点)A的坐标为(﹣1,1),左上角格点B的坐标为(﹣4,4),若分布在过定点(﹣1,0)的直线y=﹣k(x+1)两侧的格点数相同,则k的取值可以是( )

A.![]() B.
B.![]() C.2D.
C.2D.![]()
【答案】B
【解析】
由直线解析式可知:该直线过定点(﹣1,0),画出图形,由图可知:在直线CD和直线CE之间,两侧格点相同,再根据E、D两点坐标求k的取值
解:∵直线y=﹣k(x+1)过定点(﹣1,0),分布在直线y=﹣k(x+1)两侧的格点数相同,
由正方形的对称性可知,直线y=﹣k(x+1)两侧的格点数相同,
∴在直线CD和直线CE之间,两侧格点相同,(如图)
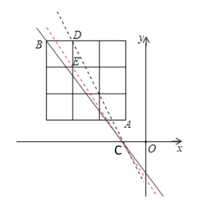
∵E(﹣3,3),D(﹣3,4),
∴﹣2<﹣k<﹣![]() ,则
,则![]() <k<2.
<k<2.
故选:B.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
【题目】甲、乙两人参加理化实验操作测试,学校进行了6次模测试,成绩如表所示:(单位:分)
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 平均分 | 众数 | |
甲 | 7 | 9 | 9 | 9 | 10 | 10 | 9 | 9 |
乙 | 7 | 8 | 9 | 10 | 10 | 10 | a | b |
(1)根据图表信息,求表格中a,b的值;
(2)已知甲的成绩的方差等于1,请计算乙的成绩的方差;
(3)从平均数和方差相结合看,分析谁的成绩好些?