题目内容
【题目】如图,在平行四边形ABCD中,AE平分∠DAB,已知CE=6,BE=8,DE=10.
(1)求BC的长;
(2)若∠CBE=36°,求∠ADC.
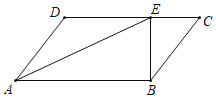
【答案】(1)BC=10;(2)126°.
【解析】
(1)依据DC∥AB,可得∠DEA=∠EAB,依据AE平分∠DAB,可得∠DAE=∠EAB,再根据∠DAE=∠DEA,即可得到AD=DE=10,进而得出BC=10;
(2)依据勾股定理的逆定理即可得出∠BEC=90°,再根据三角形内角和定理得出∠C的度数,进而得到∠ADC的度数.
解:(1)∵四边形ABCD是平行四边形,
∴AD=BC,DC∥AB,
∴∠DEA=∠EAB,
∵AE平分∠DAB,
∴∠DAE=∠EAB,
∴∠DAE=∠DEA,
∴AD=DE=10,
∴BC=10;
(2)∵CE=6,BE=8,BC=10,
∴CE2+BE2=62+82=100=BC2,
∴△BCE是直角三角形,且∠BEC=90°,
∴∠C=90°﹣∠CBE=90°﹣36°=54°,
∵AD∥BC,
∴∠D=180°﹣∠C=180°﹣54°=126°.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目