Question

【题目】为践行“绿水青山就是金山银山”的理念，及时推广生态文明建设，某校组织全校师生参与植树节活动．为调査栽种的柳树的成活情况，对全校学生的植树情况进行了抽样调查，并将调查结果分为“A．优良”“B．合格”C．差”三类．

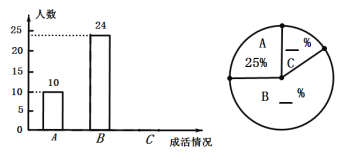
请根据图中信息，解答下列问题．

(1)求被调查学生的人数．

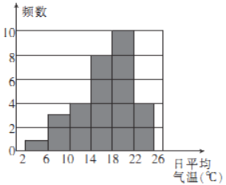
(2)将上面的条形统计图与扇形统计图补充完整．

(3)已知植树小组“勤奋组”的4名学生所种的四棵树中(每棵树对应一名责任人)，A类1棵，B类2棵，C类1棵，该小组恰好有两棵树被抽査，求恰好是两棵B类树被抽查的概率．

Answer 1

【答案】（1）40（2）见解析（3）

【解析】

（1）由A类人数及其所占百分比可得总人数；

（2）总人数减去A、B的人数求得C类人数，再分别用B、C的人数除以总人数可得对应百分比，据此即可补全图形；

（3）列表得出所有等可能结果，再根据概率公式求解可得．

（1）全班学生总人数为10÷25%=40（人）；

（2）∵C类人数为40-（10+24）=6，

∴C类所占百分比为×100%=15%，B类百分比为×100%=60%，

补全图形如下：

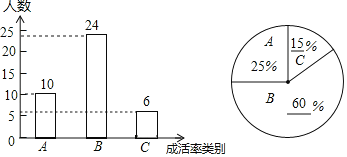
（3）列表如下：

	A	B	B	C
A		BA	BA	CA
B	AB		BB	CB
B	AB	BB		CB
C	AC	BC	BC

由表可知，共有12种等可能结果，其中全是B类的有2种情况，

所以全是B类学生的概率为．