题目内容
如图,已知抛物线y=
x2+bx与直线y=2x交于点O(0,0),A(a,12).点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E.
(1)求抛物线的函数解析式;
(2)若点C为OA的中点,求BC的长;
(3)以BC,BE为边构造矩形BCDE,设点D的坐标为(m,n),求出m,n之间的关系式.

| 1 |
| 2 |
(1)求抛物线的函数解析式;
(2)若点C为OA的中点,求BC的长;
(3)以BC,BE为边构造矩形BCDE,设点D的坐标为(m,n),求出m,n之间的关系式.

(1)∵点A(a,12)在直线y=2x上,
∴12=2a,
解得:a=6,
又∵点A是抛物线y=
x2+bx上的一点,
将点A(6,12)代入y=
x2+bx,可得b=-1,
∴抛物线解析式为y=
x2-x.
(2)∵点C是OA的中点,
∴点C的坐标为(3,6),
把y=6代入y=
x2-x,
解得:x1=1+
,x2=1-
(舍去),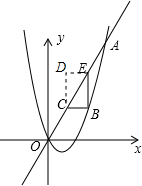
故BC=1+
-3=
-2.
(3)∵直线OA的解析式为:y=2x,
点D的坐标为(m,n),
∴点E的坐标为(
n,n),点C的坐标为(m,2m),
∴点B的坐标为(
n,2m),
把点B(
n,2m)代入y=
x2-x,可得m=
n2-
n,
∴m、n之间的关系式为m=
n2-
n.
∴12=2a,
解得:a=6,
又∵点A是抛物线y=
| 1 |
| 2 |
将点A(6,12)代入y=
| 1 |
| 2 |
∴抛物线解析式为y=
| 1 |
| 2 |
(2)∵点C是OA的中点,
∴点C的坐标为(3,6),
把y=6代入y=
| 1 |
| 2 |
解得:x1=1+
| 13 |
| 13 |

故BC=1+
| 13 |
| 13 |
(3)∵直线OA的解析式为:y=2x,
点D的坐标为(m,n),
∴点E的坐标为(
| 1 |
| 2 |
∴点B的坐标为(
| 1 |
| 2 |
把点B(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 16 |
| 1 |
| 4 |
∴m、n之间的关系式为m=
| 1 |
| 16 |
| 1 |
| 4 |

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目

 角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由. 点C,B的横坐标,且此抛物线过点A(3,6).
点C,B的横坐标,且此抛物线过点A(3,6).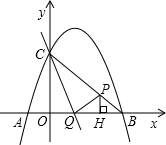 0,3)的直线y=-
0,3)的直线y=-
