题目内容
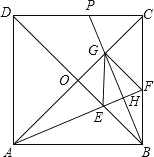
【题目】如图,已知抛物线y=ax2﹣x+c的对称轴为直线x=1,与x轴的一个交点为A(﹣1,0),顶点为B.点C(5,m)在抛物线上,直线BC交x轴于点E.
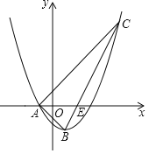
(1)求抛物线的表达式及点E的坐标;
(2)联结AB,求∠B的正切值;
(3)点G为线段AC上一点,过点G作CB的垂线交x轴于点M(位于点E右侧),当△CGM与△ABE相似时,求点M的坐标.
【答案】(1)![]() ,E(2,0);(2)3;(3) M点的坐标为(5,0)或(7,0)
,E(2,0);(2)3;(3) M点的坐标为(5,0)或(7,0)
【解析】
(1)由对称轴可求得a的值,再把A点坐标代入可求得c的值,则可求得抛物线表达式,则可求出B、C的坐标,由待定系数法可求得直线BC的解析式,可求出E的坐标
(2)由A、B、C三点的坐标可求得AB、AC和BC的长,可判定△ABC是以BC为斜边的直角三角形,利用三角形的定义可求出答案
(3)设M(x,0),当∠GCM=∠BAE时,可知△AMC为等腰直角三角形,可求的M点的坐标;当∠CMG=∠BAE时,可证得△MEC∽△MCA,利用相似三角形的性质可求得x的值,可求得M点的坐标
(1)∵抛物线对称轴为x=1,
∴![]() ,解得
,解得![]() ,
,
把A点坐标代入可得![]() ,解得
,解得![]() ,
,
∴抛物线表达式为![]() ,
,
∵![]() ,
,
∴B(1,﹣2),
把C(5,m)代入抛物线解析式可得![]() ,
,
∴C(5,6),
设直线BC解析式为y=kx+b,
把B、C坐标代入可得![]() ,解得
,解得![]() ,
,
∴直线BC解析式为y=2x﹣4,
令y=2可得2x﹣4=0,解得x=2,
∴E(2,0);
(2)∵A(﹣1,0),B(1,﹣2),C(5,6),
∴![]() ,
,
∴AB2+AC2=8+72=80=BC2,
∴△ABC是以BC为斜边的直角三角形,
∴![]() ;
;
(3)∵A(﹣1,0),B(1,﹣2),
∴∠CAE=∠BAE=45°,
∵GM⊥BC,
∴∠CGM+∠GCB=∠GCB+∠ABC=90°,
∴∠CGM=∠ABC,
∴当△CGM与△ABE相似时有两种情况,
设M(x,0),则C(x,2x﹣4),
①当∠GCM=∠BAE=45°时,则∠AMC=90°,
∴MC=AM,即2x﹣4=x+1,解得x=5,
∴M(5,0);
②当∠GMC=∠BAE=∠MAC=45°时,
∵∠MEC=∠AEB=∠MCG,
∴△MEC∽△MCA,
∴![]() ,即
,即![]() ,
,
∴MC2=(x﹣2)(x+1),
∵C(5,6),
∴MC2=(x﹣5)2+62=x2﹣10x+61,
∴(x﹣2)(x+1)=x2﹣10x+61,解得x=7,
∴M(7,0);
综上可知M点的坐标为(5,0)或(7,0).