Question

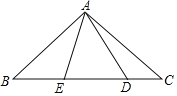
【题目】如图，在Rt△ABC 中，AB＝AC，D、E是斜边BC上两点，且∠DAE＝45°，将△ADC绕点A顺时针旋转90°后，得到△AFB．设BE＝a，DC＝b，那么AB＝_____．（用含a、b的式子表示AB）

Answer 1

【答案】

【解析】

只要证明△FAE≌△DAE，推出EF＝ED，∠ABF＝∠C＝45°，由∠EBF＝∠ABF+∠ABE＝90°，推出，可得，根据AB＝BCcos45°即可解决问题．

证明：如图，

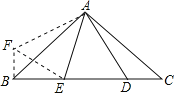
∵△DAC≌△FAB，

∴AD＝AF，∠DAC＝∠FAB，

∴∠FAD＝90°，

∵∠DAE＝45°，

∴∠DAC+∠BAE＝∠FAB+∠BAE＝∠FAE＝45°，

在△FAE和△DAE中，

，

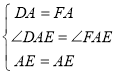∴△FAE≌△DAE，

∴EF＝ED，∠ABF＝∠C＝45°，

∵∠EBF＝∠ABF+∠ABE＝90°，

∴，

∴BC＝a+b+，

∴．

故答案为．