题目内容
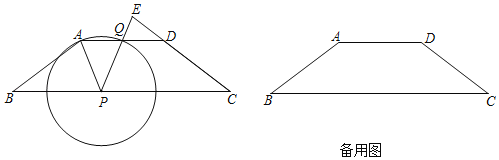
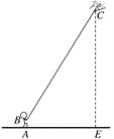
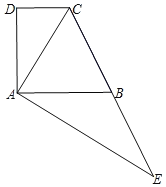
【题目】已知:如图,梯形ABCD,DC∥AB,对角线AC平分∠BCD,点E在边CB的延长线上,EA⊥AC,垂足为点A.
(1)求证:B是EC的中点;
(2)分别延长CD、EA相交于点F,若AC2=DCEC,求证:AD:AF=AC:FC.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)根据平行线的性质结合角平分线的性质可得出∠BCA=∠BAC,进而可得出BA=BC,根据等角的余角相等结合等角对等边,即可得出AB=BE,进而可得出BE=BA=BC,此题得证;
(2)根据AC2=DCEC结合∠ACD=∠ECA可得出△ACD∽△ECA,根据相似三角形的性质可得出∠ADC=∠EAC=90°,进而可得出∠FDA=∠FAC=90°,结合∠AFD=∠CFA可得出△AFD∽△CFA,再利用相似三角形的性质可证出AD:AF=AC:FC.
(1)∵DC∥AB,∴∠DCA=∠BAC.
∵AC平分∠BCD,∴∠BCA=∠BAC=∠DCA,∴BA=BC.
∵∠BAC+∠BAE=90°,∠ACB+∠E =90°,∴∠BAE=∠E,∴AB=BE,∴BE=BA=BC,∴B是EC的中点;
(2)∵AC2=DCEC,∴![]() .
.
∵∠ACD=∠ECA,∴△ACD∽△ECA,∴∠ADC=∠EAC=90°,∴∠FDA=∠FAC=90°.
又∵∠AFD=∠CFA,∴△AFD∽△CFA,∴AD:AF=AC:FC.

练习册系列答案
相关题目