题目内容
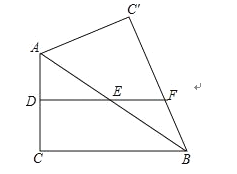
【题目】如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,联结DE并延长至点F,使EF=AE,联结AF,CF,联结BE并延长交CF于点G.
(1)求证:BC=DF;
(2)若BD=2DC,求证:GF=2EG;

【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)先证明△CDE是等边三角形,再根据∠CDE=∠ABC=60°推出DF∥AB,然后根据![]() 推出AF∥BC,从而得出四边形ABDF是平行四边形,于是AB=DF,进一步即得结论;
推出AF∥BC,从而得出四边形ABDF是平行四边形,于是AB=DF,进一步即得结论;
(2)先用SAS证明△BCE≌△FDC,从而得∠CBE=∠DFC,再证△BDE∽△FGE,于是可得![]() ,进一步即可证得结论.
,进一步即可证得结论.
证明:(1)∵△ABC是等边三角形,
∴AB=AC=BC,∠ABC=∠ACB=60°,
∵CD=CE,∴△CDE是等边三角形,
∴∠CDE=∠ABC=60°,∴DF∥AB,
∵EF=AE,DE=CE,∴![]() ,∴AF∥BC,
,∴AF∥BC,
∴四边形ABDF是平行四边形,∴AB=DF,
又∵AB=BC,∴BC=DF;
(2)∵△CDE是等边三角形,∴∠CDE=∠DCE=60°,CE=CD=DE,
又∵BC=DF,∴△BCE≌△FDC(SAS),∴∠CBE=∠DFC,
又∵∠BED=∠FEG,∴△BDE∽△FGE,∴![]() ,
,
又∵CD=DE,BD=2CD,∴![]() ,
,
∴GF=2EG.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目