题目内容
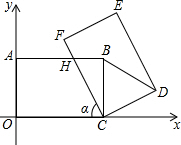 如图,在平面直角坐标系xOy中,把矩形COAB绕点C顺时针旋转α角,得到矩形CFED.设FC与AB交于点H,且A(0,n)(n>0),且3OA=2OC(如图).
如图,在平面直角坐标系xOy中,把矩形COAB绕点C顺时针旋转α角,得到矩形CFED.设FC与AB交于点H,且A(0,n)(n>0),且3OA=2OC(如图).(1)当α=60°时,求直线FC的解析式;
(2)若矩形OCBA的对称中心M,请探究:当旋转α角满足什么条件时,经过点M,且以点B为顶点的抛物线经过点D?
考点:二次函数综合题
专题:压轴题
分析:(1)先求出OC的长,写出点C的坐标,根据旋转的性质可得CF=OC,过点F作FG⊥OC于G,解直角三角形求出FG、CG的长,然后求出OG的长度,从而得到点F的坐标,再利用待定系数法求一次函数解析式解答;
(2)根据矩形的性质求出点M的坐标,再求出点B的坐标,然后利用顶点式形式求出抛物线的解析式,过点D作DN⊥x轴于N,易得∠CDN=α,然后解直角三角形求出CN、DN,再求出ON,然后写出点D的坐标,然后把点D的坐标代入抛物线解析式得到关于α的三角函数的方程,求解即可得到α的值.
(2)根据矩形的性质求出点M的坐标,再求出点B的坐标,然后利用顶点式形式求出抛物线的解析式,过点D作DN⊥x轴于N,易得∠CDN=α,然后解直角三角形求出CN、DN,再求出ON,然后写出点D的坐标,然后把点D的坐标代入抛物线解析式得到关于α的三角函数的方程,求解即可得到α的值.
解答:解:(1)∵A(0,n),3OA=2OC,
∴OC=
n,
∴点C的坐标为(
n,0),
根据旋转的性质,CF=OC=
n,
过点F作FG⊥OC于G,
则FG=CF•sin60°=
n•
=
n,
CG=CF•cos60°=
n•
=
n,
∴OG=OC-CG=
n-
n=
n,
∴点F的坐标为(
n,
n),
设直线FC的解析式为y=kx+b,
则
,
解得
,
∴直线FC的解析式为y=-
x+
n;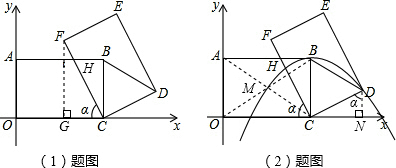
(2)∵A(0,n),C(
n,0),
∴矩形OCBA的对称中心M的坐标为(
n,
n),
点B的坐标为(
n,n),
设抛物线解析式为y=a(x-
n)2+n,
把点M的坐标代入得,a(
n-
n)2+n=
n,
解得a=-
,
所以,抛物线解析式为y=-
(x-
n)2+n,
过点D作DN⊥x轴于N,易得∠CDN=∠OCF=α,
∴CN=nsinα,DN=ncosα,
∴ON=OC+CN=
n+nsinα,
∴点D的坐标为(
n+nsinα,ncosα),
代入抛物线解析式得,-
(
n+nsinα-
n)2+n=ncosα,
整理得,8sin2α+9cosα-9=0,
∵sin2α+cos2α=1,
∴sin2α=1-cos2α,
∴8cos2α-9cosα+1=0,
解得cosα=
或cosα=1,
当cosα=1时,α=0,
∴cosα=1舍去,
因此,当旋转α角满足cosα=
时,经过点M,且以点B为顶点的抛物线经过点D.
∴OC=
| 3 |
| 2 |
∴点C的坐标为(
| 3 |
| 2 |
根据旋转的性质,CF=OC=
| 3 |
| 2 |
过点F作FG⊥OC于G,
则FG=CF•sin60°=
| 3 |
| 2 |
| ||
| 2 |
3
| ||
| 4 |
CG=CF•cos60°=
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
∴OG=OC-CG=
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
∴点F的坐标为(
| 3 |
| 4 |
3
| ||
| 4 |
设直线FC的解析式为y=kx+b,
则
|
解得
|
∴直线FC的解析式为y=-
| 3 |
3
| ||
| 2 |

(2)∵A(0,n),C(
| 3 |
| 2 |
∴矩形OCBA的对称中心M的坐标为(
| 3 |
| 4 |
| 1 |
| 2 |
点B的坐标为(
| 3 |
| 2 |
设抛物线解析式为y=a(x-
| 3 |
| 2 |
把点M的坐标代入得,a(
| 3 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
解得a=-
| 8 |
| 9n |
所以,抛物线解析式为y=-
| 8 |
| 9n |
| 3 |
| 2 |
过点D作DN⊥x轴于N,易得∠CDN=∠OCF=α,
∴CN=nsinα,DN=ncosα,
∴ON=OC+CN=
| 3 |
| 2 |
∴点D的坐标为(
| 3 |
| 2 |
代入抛物线解析式得,-
| 8 |
| 9n |
| 3 |
| 2 |
| 3 |
| 2 |
整理得,8sin2α+9cosα-9=0,
∵sin2α+cos2α=1,
∴sin2α=1-cos2α,
∴8cos2α-9cosα+1=0,
解得cosα=
| 1 |
| 8 |
当cosα=1时,α=0,
∴cosα=1舍去,
因此,当旋转α角满足cosα=
| 1 |
| 8 |
点评:本题是二次函数综合题型,主要考查了待定系数法求一次函数解析式,待定系数法求二次函数解析式,矩形的性质,解直角三角形,锐角三角函数的运算,(2)表示出点D的坐标并代入抛物线解析式进行计算难度较大,计算时要用到sin2α+cos2α=1的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
去年某市有1530人参加中考,为了了解他们的数学成绩,从中抽取200名考生的数学成绩,其中有62名考生达到优秀,那么该市约有多少名考生达到优秀( )
| A、500名 | B、475名 |
| C、450名 | D、400名 |
函数y=1-|x-x2|的图象是( )
A、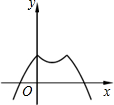 |
B、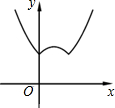 |
C、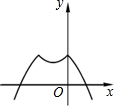 |
D、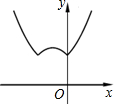 |
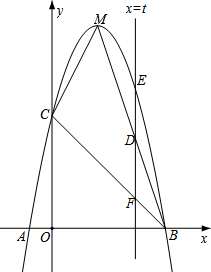 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,其中A点坐标为(-1,0),线段AB=6,
如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,其中A点坐标为(-1,0),线段AB=6, 如图,已知抛物线y=ax2+bx+c与y轴交于A(0,4),且抛物线经过点C(-3,-2),对称轴x=-
如图,已知抛物线y=ax2+bx+c与y轴交于A(0,4),且抛物线经过点C(-3,-2),对称轴x=-