题目内容
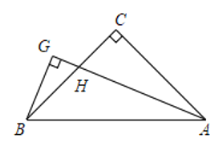
【题目】如图,在△ABC中,∠C=90°,CA=CB, AG平分∠BAC交BC于H,BG⊥AG,垂足为G.若AH=8,则BG的长为( )
A.3B.5C.8D.4
【答案】D
【解析】
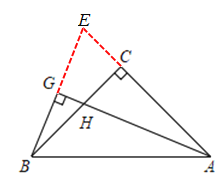
如图,延长AC交BG的延长线于E,构建等腰△BAE、全等三角形△BEC和△AHC,利用等腰三角形的性质和全等三角形的对应边相等得到:BE=AH,所以BG=![]() AH=4.
AH=4.
如图,延长AC交BG的延长线于E,
∵△ABC中,∠C=90°,CA=CB,
∴∠ABC=∠CAB=45°,
∵AG平分∠BAC
∴∠CAG=![]() ∠BAC=22.5°,
∠BAC=22.5°,
∵AG⊥BG,
∴∠BGA=90°,
∴∠GBA=90°-22.5°=67.5°,
∴∠GBC=∠EBA-∠ABC=22.5°.
∴∠GBC=∠CAH,
∵CA=CB,∠ACB=∠BCE
∴△ACH≌△BCE
∴BE=AH
∵AG平分∠BAC, AG⊥BG,
∴BG=EG,即BG=![]() BE,
BE,
∴BG=![]() AH=
AH=![]() ×8=4.
×8=4.
故选:D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】车间有20名工人,某天他们生产的零件个数统计如下表.
车间20名工人某一天生产的零件个数统计表
生产零件的个数(个) | 9 | 10 | 11 | 12 | 13 | 15 | 16 | 19 | 20 |
工人人数(人) | 1 | 1 | 6 | 4 | 2 | 2 | 2 | 1 | 1 |
(1)求这一天20名工人生产零件的平均个数;
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施.如果你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?




