Question

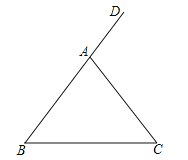
【题目】如图，在△ABC中，AB=AC，∠DAC是△ABC的一个外角．

实验与操作：

根据要求进行尺规作图，并在图中标明相应字母（保留作图痕迹，不写作法）

（1）作∠DAC的平分线AM；

（2）作线段AC的垂直平分线，与AM交于点F，与BC边交于点E，连接AE，CF．

猜想并判断四边形AECF的形状并加以证明．

Answer 1

【答案】（1）作图见试题解析；（2）作图见试题解析，四边形AECF的形状为菱形．

【解析】

试题分析：先作以个角的交平分线，再作线段的垂直平分线得到几何图形，由AB=AC得∠ABC=∠ACB，由AM平分∠DAC得∠DAM=∠CAM，则利用三角形外角性质可得∠CAM=∠ACB，再根据线段垂直平分线的性质得OA=OC，∠AOF=∠COE，于是可证明△AOF≌△COE，所以OF=OE，然后根据菱形的判定方法易得四边形AECF的形状为菱形．

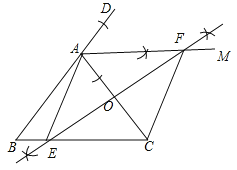
试题解析：解：如图所示，四边形AECF的形状为菱形．理由如下：

∵AB=AC，∴∠ABC=∠ACB，∵AM平分∠DAC，∴∠DAM=∠CAM，而∠DAC=∠ABC+∠ACB，∴∠CAM=∠ACB，∴EF垂直平分∠AC，∴OA=OC，∠AOF=∠COE，在△AOF和△COE中，∵∠FAO=∠ECO，OA=OC，∠AOF=∠COE，∴△AOF≌△COE，∴OF=OE，即AC和EF互相垂直平分，∴四边形AECF的形状为菱形．