题目内容
【题目】已知抛物线![]() (
(![]() 为常数).
为常数).
(1)当该抛物线经过坐标原点,并且顶点在第四象限时,求出它所对应的函数关系式;
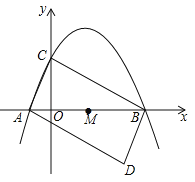
(2)设![]() 是(1)所确定的抛物线上位于
是(1)所确定的抛物线上位于![]() 轴下方、且在对称轴左侧的一个动点,过
轴下方、且在对称轴左侧的一个动点,过![]() 作
作![]() 轴的平行线,交抛物线于另一点
轴的平行线,交抛物线于另一点![]() ,再作
,再作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() .
.
①当![]() 时,求矩形
时,求矩形![]() 的周长;
的周长;
②试问矩形![]() 的周长是否存在最大值?如果存在,请求出这个最大值,并指出此时
的周长是否存在最大值?如果存在,请求出这个最大值,并指出此时![]() 点的坐标.如果不存在,请说明理由.
点的坐标.如果不存在,请说明理由.
【答案】(1)y=x2-3x;(2)①6;②存在;最大值为![]() ,此时A(
,此时A(![]() ,
,![]() )
)
【解析】
(1)将原点坐标代入抛物线的解析式中,即可求出n的值,然后根据抛物线顶点在第四象限将不合题意的n值舍去,即可得出所求的二次函数解析式;
(2)①先根据抛物线的解析式求出抛物线与x轴另一交点E的坐标,根据抛物线和矩形的对称性可知:OB的长,就是OE与BC的差的一半,由此可求出OB的长,即B点的坐标,然后代入抛物线的解析式中即可求出B点纵坐标,也就得出了矩形AB边的长.进而可求出矩形的周长;
②可设出A点坐标(设横坐标,根据抛物线的解析式表示纵坐标),也就能表示出B点的坐标,即可得出OB的长,同①可得出BC的长,而AB的长就是A点纵坐标的绝对值,由此可得出一个关于矩形周长和A点纵坐标的函数关系式,根据函数的性质可得出矩形周长的最大值及对应的A的坐标.
解:(1)由已知条件,得n2-1=0,
解这个方程,得n1=1,n2=-1,
当n=1时,得y=x2+x,此抛物线的顶点不在第四象限,
当n=-1时,得y=x2-3x,此抛物线的顶点在第四象限,
∴所求的函数关系为y=x2-3x;
(2)由y=x2-3x,
令y=0,得x2-3x=0,
解得x1=0,x2=3,
∴抛物线与x轴的另一个交点为(3,0),
∴它的顶点为(![]() ,
,![]() ),对称轴为直线x=
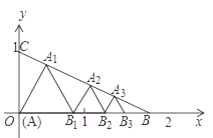
),对称轴为直线x=![]() ,其大致位置如图所示,
,其大致位置如图所示,
①∵BC=1,易知OB=![]() ×(3-1)=1,
×(3-1)=1,
∴B(1,0),
∴点A的横坐标x=1,又点A在抛物线y=x2-3x上,
∴点A的纵坐标y=12-3×1=-2.
∴AB=|y|=|-2|=2,
∴矩形ABCD的周长为:2(AB+BC)=2×(2+1)=6;
②∵点A在抛物线y=x2-3x上,故可设A点的坐标为(x,x2-3x),
∴B点的坐标为(x,0)(0<x<![]() )
)
∴BC=3-2x,A在x轴下方,
∴x2-3x<0,
∴AB=|x2-3x|=3x-x2
∴矩形ABCD的周长,
C=2[(3x-x2)+(3-2x)]=-2(x-![]() )2+
)2+![]() ,
,
∵a=-2<0,抛物线开口向下,二次函数有最大值,
∴当x=![]() 时,矩形ABCD的周长C最大值为
时,矩形ABCD的周长C最大值为![]() ,
,
此时点A的坐标为A(![]() ,
,![]() ).
).