题目内容
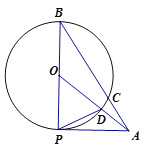
【题目】如图,抛物线y=﹣![]() x2+
x2+![]() x+2与x轴交于点A,B,与y轴交于点C.
x+2与x轴交于点A,B,与y轴交于点C.
(1)试求A,B,C的坐标;
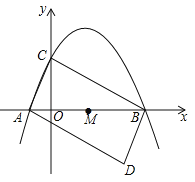
(2)将△ABC绕AB中点M旋转180°,得到△BAD.3
①求点D的坐标;
②判断四边形ADBC的形状,并说明理由;
(3)在该抛物线对称轴上是否存在点P,使△BMP与△BAD相似?若存在,请直接写出所有满足条件的P点的坐标;若不存在,请说明理由.
【答案】(1) A(﹣1,0),B(4,0),C(0,2);(2)①D(3,﹣2);②四边形ADBC是矩形;理由见解析,(3) 点P的坐标为:(1.5,1.25),(1.5,﹣1.25),(1.5,5),(1.5,﹣5).
![]()
【解析】
试题分析:(1)直接利用y=0,x=0分别得出A,B,C的坐标;
(2)①利用旋转的性质结合三角形各边长得出D点坐标;
②利用平行四边形的判定方法结合勾股定理的逆定理得出四边形ADBC的形状;
(3)直接利用相似三角形的判定与性质结合三角形各边长进而得出答案.
试题解析:(1)当y=0时,0=﹣![]() x2+
x2+![]() x+2,
x+2,
解得:x1=﹣1,x2=4,
则A(﹣1,0),B(4,0),
当x=0时,y=2,
故C(0,2);
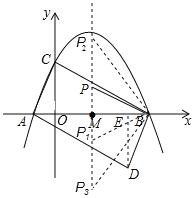
(2)①过点D作DE⊥x轴于点E,
∵将△ABC绕AB中点M旋转180°,得到△BAD,
∴DE=2,AO=BE=1,OM=ME=1.5,
∴D(3,﹣2);
②∵将△ABC绕AB中点M旋转180°,得到△BAD,
∴AC=BD,AD=BC,
∴四边形ADBC是平行四边形,
∵AC=![]() ,BC=
,BC=![]() ,AB=5,
,AB=5,
∴AC2+BC2=AB2,
∴△ACB是直角三角形,
∴∠ACB=90°,
∴四边形ADBC是矩形;
(3)由题意可得:BD=![]() ,AD=2
,AD=2![]() ,
,
则![]() ,
,
当△BMP∽△ADB时,
![]() ,
,
可得:BM=2.5,
则PM=1.25,
故P(1.5,1.25),
当△BMP1∽△ABD时,
P1(1.5,﹣1.25),
当△BMP2∽△BDA时,
可得:P2(1.5,5),
当△BMP3∽△BDA时,
可得:P3(1.5,﹣5),
综上所述:点P的坐标为:(1.5,1.25),(1.5,﹣1.25),(1.5,5),(1.5,﹣5).

 阅读快车系列答案
阅读快车系列答案