题目内容
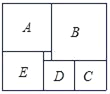
【题目】如图是由6个正方形拼成的一个长方形,如果最小的正方形的边长为1
(Ⅰ)能否求出拼成的长方形的面积?____(填“能”或“不能”);
(Ⅱ)若能,请你写出拼成的长方形的面积;若不能,请说明理由.

【答案】(Ⅰ)能;(II)拼成的长方形的面积为143.
【解析】
(I)能够求出拼成的长方形的面积;
(II)设正方形C,D的边长为x,则正方形A的边长为(x+2),正方形B的边长为(x+3),正方形的E的边长为(x+1),由长方形的对边相等,可得出关于x的一元一次方程,解之即可求出x的值,再利用长方形的面积公式即可求出结论.
(Ⅰ)能.
(II)如图,将各正方形标上序号.
设正方形C,D的边长为x,则正方形A的边长为(x+2),正方形B的边长为(x+3),正方形的E的边长为(x+1),
依题意,得:2x+x+1=x+2+x+3,
解得:x=4.
∴(2x+x+1)(x+2+x+1)=13×11=143.
答:拼成的长方形的面积为143.

练习册系列答案
相关题目