题目内容
【题目】如图，一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点，则函数y=ax2+（b﹣1）x+c的图象可能是（ ）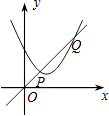
A.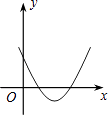
B.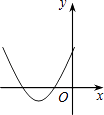
C.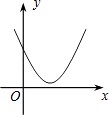
D.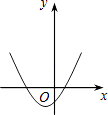
【答案】A
【解析】解：∵一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点，
∴方程ax2+（b﹣1）x+c=0有两个不相等的根，
∴函数y=ax2+（b﹣1）x+c与x轴有两个交点，
又∵﹣ 
＞0，a＞0
∴﹣ 
=﹣ + 
＞0
∴函数y=ax2+（b﹣1）x+c的对称轴x=﹣ ＞0，
∴A符合条件，
故选A．
由一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点，得出方程ax2+（b﹣1）x+c=0有两个不相等的根，进而得出函数y=ax2+（b﹣1）x+c与x轴有两个交点，根据方程根与系数的关系得出函数y=ax2+（b﹣1）x+c的对称轴x=﹣ ＞0，即可进行判断．
练习册系列答案
全能测控一本好卷系列答案
发散思维新课堂系列答案
相关题目
