题目内容
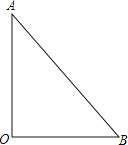
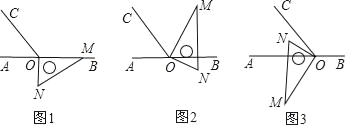
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=112°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,问:射线ON是否平分∠AOC?请说明理由;
(2)将图1中的三角板绕点O按每秒4°的速度沿逆时针方向旋转至图3,使射线ON恰好平分锐角∠AOC,求此时旋转一共用了多少时间?
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
【答案】(1)平分,理由见解析;(2)此时旋转一共用了59秒;(3)∠AOM﹣∠NOC=22°,理由见解析
【解析】
(1)延长NO到点D,先得出∠MOB为直角,再利用∠MOB和∠MOC,可分别求出∠NOB和∠COD的大小,最后求出∠AOD的大小,得到平分;
(2)先求出旋转的角度,然后用角度除速度即可;
(3)∠AOM和∠NOC都用含∠AON的式子表示出来,代入抵消可得结果
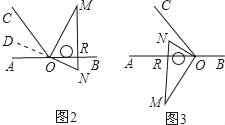
解:(1)平分,理由:延长NO到D,
∵∠MON=90°∴∠MOD=90°
∴∠MOB+∠NOB=90°,
∠MOC+∠COD=90°,
∵∠MOB=∠MOC=56° ∴∠NOB=∠COD=34°,
∵∠AOD=180°-∠BOC-∠COD=34°,
∴∠COD=∠AOD, ∴直线NO平分∠AOC;
(2)如图3,当NO平分∠AOC时,∠NOA=34°,
∴∠AOM=56°, 即逆时针旋转的角度为:180°+56°=236°,
由题意得,236÷4=59(秒)
答:此时旋转一共用了59秒
(3)∠AOM﹣∠NOC=22°,
理由:∵∠AOM=90°﹣∠AON ∠NOC=68°﹣∠AON,
∴∠AOM﹣∠NOC
=(90°﹣∠AON)﹣(68°﹣∠AON)
=22°.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案【题目】为了激发学生爱数学、学数学、用数学的热情,某学校在七年级开展“魅力数学”趣味竞赛,该校七年级共有学生400人参加竞赛.现随机抽取40名参赛学生的成绩数据(百分制)进行整理、描述和分析.
74 97 96 89 98 74 69 76 72 78
99 72 97 76 99 74 99 73 98 74
76 88 93 65 78 94 89 68 95 50
89 88 89 89 77 94 87 88 92 91
范围 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
频数 | 1 | m | 13 | 9 | 14 |
平均数、中位数、众数如下表所示:
平均数 | 中位数 | 众数 |
84.1 | n | 89 |
根据以上信息,回答下列问题:
(1)m= ,n= ;
(2)小明说:“这次竞赛我得了84分,在所有参赛学生中排名属中等偏上!”小明的说法 (填“正确”或“不正确”),理由是 ;
(3)若成绩不低于85分可以进入决赛,估计参赛的400名学生中能进入决赛的人数.
【题目】某网站策划了A、B两种上网的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
A | 30 | 25 | 0.05 |
B | m | n | P |
设每月上网学习时间为x(h)小时,方案A,B的收费金额分别为yA (元)、yB(元).
如图是yB与x之间函数关系的图象
(友情提示:若累计上网时间不超出“包时上网时间”,则只收”月使用费“;若累计上网时间不超出“包时上网时间”,则对超出部分再加收”超时费“)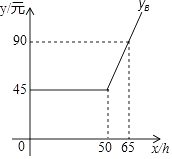
(1)m=;n=p= .
(2)写出yA与x之间的函数关系式.
(3)若每月上网的时间为29小时,请说明选取哪种方式能节省上网费?