题目内容
【题目】已知△ABC是边长为4的等边三角形,BC在x轴上,点D为BC的中点,点A在第一象限内,AB与y轴的正半轴交与点E,已知点B(﹣1,0).
(1)点A的坐标: ,点E的坐标: ;
(2)若二次函数y=﹣![]() x2+bx+c过点A、E,求此二次函数的解析式;
x2+bx+c过点A、E,求此二次函数的解析式;
(3)P是线段AC上的一个动点(P与点A、C不重合)连结PB、PD,设L是△PBD的周长,当L取最小值时。
求:①点P的坐标
②判断此时点P是否在(2)中所求的抛物线上,请充分说明你的判断理由.

【答案】(1)E(0, ![]() );(2)y=﹣
);(2)y=﹣![]() x2+
x2+![]() x+
x+![]() ;(3)①P(
;(3)①P(![]() ,
, ![]() ),②此时点P在抛物线上.
),②此时点P在抛物线上.
【解析】试题分析:
(1)由已知条件求得线段OD、AD、OE的长可得点A、E的坐标;
(2)把(1)中所求得的A、E坐标代入![]() 中列方程组求得
中列方程组求得![]() 的值可得抛物线的解析式;
的值可得抛物线的解析式;
(3)由△PBD中,BD边是定值可知当PB+PD最小时,△PBD的周长最小,因此作点D关于AC的对称点D’,连接BD’,交AC于点P,此时,△PBD的周长最小.①作D’G⊥![]() 轴,连接DD’交AC于点F,利用轴对称和等边三角形的性质求得DG、D’G的长可得D’的坐标,用待定系数法求得直线DD’和AC的解析式就可求得点P的坐标;②把所求得的点P的坐标代入(2)中所得抛物线的解析式可判断点P是否在该抛物线上.
轴,连接DD’交AC于点F,利用轴对称和等边三角形的性质求得DG、D’G的长可得D’的坐标,用待定系数法求得直线DD’和AC的解析式就可求得点P的坐标;②把所求得的点P的坐标代入(2)中所得抛物线的解析式可判断点P是否在该抛物线上.
试题解析:
(1)连接AD,如图1,
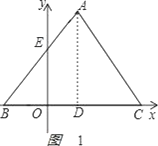
∵△ABC是边长为4的等边三角形,又B的坐标为(﹣1,0),BC在x轴上,A在第一象限,
∴点C在x轴的正半轴上,
∴C的坐标为(3,0),由中点坐标公式,得:D的坐标为(1,0).
∵D为BC的中点,AB=AC=BC=4,
∴AD⊥BC,
∴AD=![]() ,
,
∴A的坐标是(1, ![]() ).
).
∵在△BOE中,∠BOE=90°,∠EBO=60°,
∴∠BEO=30°,
∴BE=2BO=2,
∴OE=![]() ,
,
∴点E的坐标为(0, ![]() );
);
(2)∵抛物线![]() 过点A、E,
过点A、E,
∴ ,解得:
,解得: ![]() ,
, ![]() ,
,
∴抛物线的解析式为![]() ;
;
(3)作点D关于AC的对称点D',
连接BD'交AC于点P,则PB与PD的和取最小值,
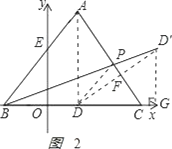
即△PBD的周长L取最小值,如图2.
①∵D、D′关于直线AC对称,
∴DD′⊥AC,∴∠DFC=90°,∵∠ACD=60°,∴∠D′DC=30°,
∴在Rt△DFC中,DF= ![]() =
=![]() ,∴DD'=
,∴DD'=![]() ,
,
作D’G⊥![]() 轴于点G,
轴于点G,
在Rt△D’DG中,DG=D’D![]() cos30°=3,DG=D’D
cos30°=3,DG=D’D![]() sin30°=
sin30°=![]() ,
,
∴点D'的坐标为(4, ![]() ),
),
∴由待定系数法可求得:直线BD'的解析式为: ![]() ,直线AC的解析式为:
,直线AC的解析式为: ![]() ,
,
由 解得:
解得: 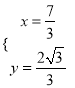 ,
,
∴点P的坐标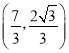 .
.
②∵在![]() 中,当
中,当![]() 时,
时, ![]() ,
,
∴点P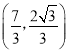 在抛物线上.
在抛物线上.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案