题目内容
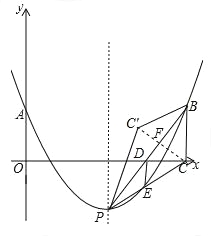
【题目】如图，抛物线y=
（其中m＞1）与其对称轴l相交于点P，与y轴相交于点A（0，m）．点A关于直线l的对称点为B，作BC⊥x轴于点C，连接PC、PB，与抛物线、x轴分别相交于点D、E，连接DE．将△PBC沿直线PB翻折，得到△PBC′．
（1）该抛物线的解析式为 ； （用含m的式子表示）；
（2）探究线段DE、BC的关系，并证明你的结论；
（3）直接写出C′点的坐标（用含m的式子表示）．
【答案】(1)y=
；(2)DE=
BC，理由详见解析；(3)（
，
）．
【解析】
试题分析：（1）将点A的坐标代入抛物线解析式，即可求出a的值；
（2）根据抛物线的解析式，求出顶点P的坐标，根据对称轴，求出点B，C的坐标，根据待定系数法求出直线BP、CP的解析式，求出点D、E的坐标，进而求出DE，BC的长度，即可解得；
（3）连接CC′交直线BP于点F，则CC′⊥BP，且CF=C′F，求出CC′的解析式，进而求得点F的坐标，根据CF=C′F，即可解答．
试题解析：（1）把点A（0，m）代入y=
，
得：
﹣m=m，
am﹣1=0，
∵am＞1，
∴a=
，
∴y=，
故答案为：y=；
（2）DE=BC．
理由：又抛物线y=，可得抛物线的顶点坐标P（
，﹣m），
由l：x=，可得：点B（
，m），
∴点C（，0）．
设直线BP的解析式为y=kx+b，点P（，﹣m）和点B（，m）在这条直线上，
得：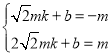
，解得：
，
∴直线BP的解析式为：y=
﹣3m，
令y=0，﹣3m=0，解得：x=
，
∴点D（，0）；
设直线CP的解析式为y=
x+
，点P（
，﹣m）和点C（
，0）在这条直线上，
得：
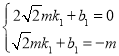，解得：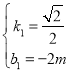
，
∴直线CP的解析式为：y=
﹣2m；
抛物线与直线CP相交于点E，可得：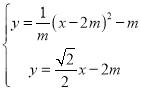
，解得：
，
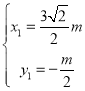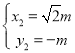（舍去），
∴点E（
，
）；
∵
，
∴DE⊥x轴，
∴DE=
=
，BC=
=m=2DE，
即DE=
BC；
（3）C′（
，
）．
连接CC′，交直线BP于点F，
∵BC′=BC，∠C′BF=∠CBF，
∴CC′⊥BP，CF=C′F，
设直线BP的解析式为y=kx+b，点B（
，m），P（
，﹣m）在直线上，
∴
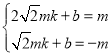，解得：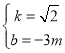
，
∴直线BP的解析式为：y=
﹣3m，
∵CC′⊥BP，
∴设直线CC′的解析式为：y=
，
∴
，解得：
=2m，
联立①②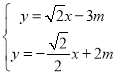，得：
，解得：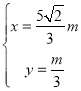
，
∴点F（
，
），
∴CF=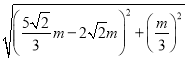
=
，
设点C′的坐标为（a，
），
∴C′F=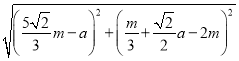
=，解得：a=，
∴=，
∴C′（，）．
