题目内容
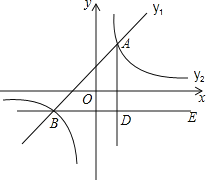
【题目】如图,二次函数![]() 的图象经过点
的图象经过点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() 为二次函数图象上任一点.
为二次函数图象上任一点.
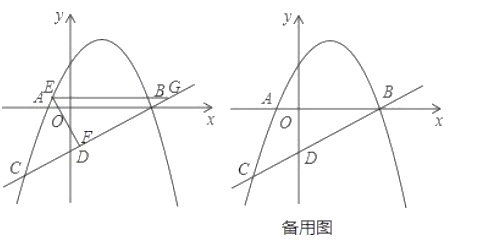
![]() 求这个二次函数的解析式;
求这个二次函数的解析式;
![]() 若点
若点![]() 是直线
是直线![]() 上方抛物线上一点,过
上方抛物线上一点,过![]() 分别作
分别作![]() 和
和![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于不同的两点
于不同的两点![]() 在
在![]() 的左侧),求
的左侧),求![]() 周长的最大值;
周长的最大值;
![]() 是否存在点
是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为直角边的直角三角形?如果存在,求点
为直角边的直角三角形?如果存在,求点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
【答案】![]() ;
;![]() 最大周长为
最大周长为![]() ;
;![]()
![]() 或
或![]() 或
或![]() .
.
【解析】
(1)运用待定系数法求这个二次函数的解析式;
(2)先求解![]() 的解析式,证明
的解析式,证明![]() 得到
得到![]() 利用
利用![]() 的坐标表示
的坐标表示![]() 的长度,利用三角函数求解
的长度,利用三角函数求解![]() 的长度,建立周长与
的长度,建立周长与![]() 的横坐标之间的函数关系式,利用函数的最值求周长的最大值,
的横坐标之间的函数关系式,利用函数的最值求周长的最大值,
(3)分情况讨论:以![]() 为直角顶点,利用
为直角顶点,利用![]() 可直接得到答案,以
可直接得到答案,以![]() 为直角顶点时,利用
为直角顶点时,利用![]() 求解
求解![]() 的解析式,联立一次函数与二次函数的解析式可得答案.
的解析式,联立一次函数与二次函数的解析式可得答案.
解:(1)![]()
![]()
![]() 设抛物线为:
设抛物线为:![]()
把![]() 代入
代入![]()
![]()
![]()
![]()
(2)设直线![]() 为
为![]()
![]()
解得:![]()
![]()
![]()
![]()
![]()
![]() 轴,
轴,![]() 轴,
轴,
![]()
设![]()
![]()
![]()
![]()
![]()
![]() 的周长
的周长![]()
当![]() 时,
时,![]() 周长最大.
周长最大.
最大周长为:![]()
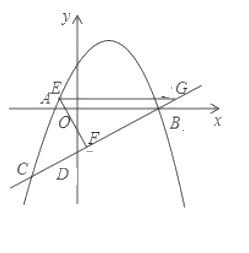
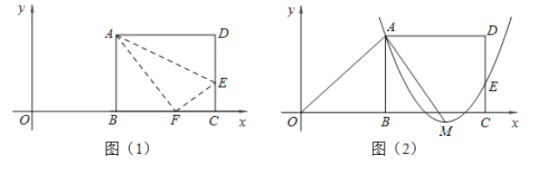
(3)如图,当![]() 时,
时,
![]()
![]()
![]() 为抛物线与
为抛物线与![]() 轴的交点,
轴的交点,
![]()
当![]() 时,
时,![]() 与
与![]() 轴交于
轴交于![]() 点,
点,
![]()
![]()
![]()
![]()
![]()
设![]() 的解析式为:
的解析式为:![]()
![]()
解得:![]()
![]() 为
为![]()
![]()
解得: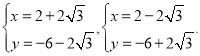
![]() 或
或![]()
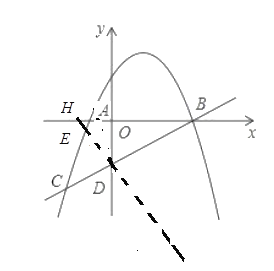
综上:![]() 以
以![]() 为直角边的直角三角形时,点
为直角边的直角三角形时,点![]() 坐标为
坐标为![]() 或
或![]() 或
或![]() .
.

练习册系列答案
相关题目