题目内容
 如图,抛物线与x轴交于A(-2,0),B(6,0)两点,与y轴交于点C(0,-4).
如图,抛物线与x轴交于A(-2,0),B(6,0)两点,与y轴交于点C(0,-4).(1)求抛物线的解析式;
(2)点M是线段AB上的一个动点,过点M作MN∥BC,交AC于点N,连接CM,当△CMN的面积最大时,求点M的坐标;
(3)点D(4,k)在(1)中抛物线上,点F为抛物线上一动点,在x轴上是否存在点F,使以A、D、E、F为顶点的四边形是平行四边形?如果存在,求出所有满足条件的点F的坐标;若不存在,请说明理由.
分析:(1)将已知点的坐标代入抛物线的交点式即可确定二次函数的解析式;
(2)首先利用m表示出线段AM的长,然后利用△AMN∽△ABC得到比例式,最后得到有关m的二次函数求最值即可;
(3)此题可分作两种情况考虑:
①AF∥DE;根据抛物线的解析式可求得C点坐标,可得C、D关于抛物线对称轴对称,即C、D的纵坐标相同,所以CD∥x轴,那么C点就是符合条件的G点,易求得CD的长,根据平行四边形的性质知BE=CD,由此可得到BE的长,将B点坐标向左或向右平移CD个单位即可得到两个符合条件的E点坐标;
②AD∥EF;根据平行四边形的性质知,此时G、D的纵坐标互为相反数,由此可求得G点的纵坐标,将其代入抛物线的解析式中即可求得G点的坐标;那么将G点的横坐标减去3(B、D横坐标差的绝对值),即可得到两个符合条件的E点坐标;
综上所述,符合条件的E点坐标应该有4个.
(2)首先利用m表示出线段AM的长,然后利用△AMN∽△ABC得到比例式,最后得到有关m的二次函数求最值即可;
(3)此题可分作两种情况考虑:
①AF∥DE;根据抛物线的解析式可求得C点坐标,可得C、D关于抛物线对称轴对称,即C、D的纵坐标相同,所以CD∥x轴,那么C点就是符合条件的G点,易求得CD的长,根据平行四边形的性质知BE=CD,由此可得到BE的长,将B点坐标向左或向右平移CD个单位即可得到两个符合条件的E点坐标;
②AD∥EF;根据平行四边形的性质知,此时G、D的纵坐标互为相反数,由此可求得G点的纵坐标,将其代入抛物线的解析式中即可求得G点的坐标;那么将G点的横坐标减去3(B、D横坐标差的绝对值),即可得到两个符合条件的E点坐标;
综上所述,符合条件的E点坐标应该有4个.
解答:解:(1)设抛物线的解析式为y=a(x+2)(x-6),
将点C的坐标带入,求得a=
.
∴抛物线的解析式为y=
x2-
x-4.
(2)设点M的坐标为(m,0),过点N作NH⊥x轴于点H(如图(1)).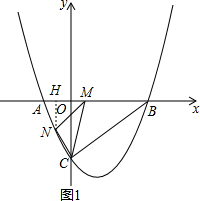
∵点A的坐标为(-2,0),点B的坐标为(6,0),
∴AB=8,AM=m+2.
∵MN∥BC,
∴△AMN∽△ABC.
∴
=
,
∴
=
,
∴NH=
∴S△CMN=S△ACM-S△AMN
=
×AM×CO-
AM×NH
=
(m+2)(4-
)
 =-
=-
m2+m+3
=-
(m-2)2+4.
∴当m=2时,S△CMN有最大值4.
此时,点M的坐标为(2,0).
(3)∵点D(4,k)在抛物线y=
x2-
x-4上,
∴当x=4时,k=-4,
∴D点的坐标是(4,-4).
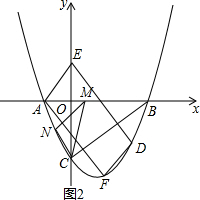
如图(2),当AF为平行四边形的边时,AF∥DE,
 ∵D(4,-4),
∵D(4,-4),
∴E(0,-4),DE=4.
∴F1(-6,0),F2(2,0).
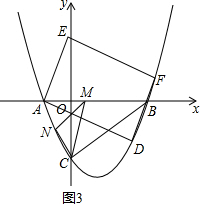
如图(3)当AF为平行四边形的对角线时,
设F(n,0),则平行四边形的对称中心为(
,0).
∴E’的坐标为(n-6,4).
把E’( n-6,4)代入y=
x2-
x-4,
得n2-16n+36=0.
解得n=8±2
.
F3(8-2
,0),F4(8+2
,0).
将点C的坐标带入,求得a=
| 1 |
| 3 |
∴抛物线的解析式为y=
| 1 |
| 3 |
| 4 |
| 3 |
(2)设点M的坐标为(m,0),过点N作NH⊥x轴于点H(如图(1)).

∵点A的坐标为(-2,0),点B的坐标为(6,0),
∴AB=8,AM=m+2.
∵MN∥BC,
∴△AMN∽△ABC.
∴
| NH |
| CO |
| AM |
| AB |
∴
| NH |
| 4 |
| m+2 |
| 8 |
∴NH=
| m+2 |
| 2 |
∴S△CMN=S△ACM-S△AMN
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| m+2 |
| 2 |
 =-
=-| 1 |
| 4 |
=-
| 1 |
| 4 |
∴当m=2时,S△CMN有最大值4.
此时,点M的坐标为(2,0).
(3)∵点D(4,k)在抛物线y=
| 1 |
| 3 |
| 4 |
| 3 |
∴当x=4时,k=-4,
∴D点的坐标是(4,-4).
如图(2),当AF为平行四边形的边时,AF∥DE,
 ∵D(4,-4),
∵D(4,-4),∴E(0,-4),DE=4.
∴F1(-6,0),F2(2,0).
如图(3)当AF为平行四边形的对角线时,
设F(n,0),则平行四边形的对称中心为(
| n-2 |
| 2 |
∴E’的坐标为(n-6,4).
把E’( n-6,4)代入y=
| 1 |
| 3 |
| 4 |
| 3 |
得n2-16n+36=0.
解得n=8±2
| 7 |
F3(8-2
| 7 |
| 7 |
点评:此题考查了二次函数解析式的确定、轴对称的性质以及平行四边形的判定和性质;要特别注意的是(3)题中,由于没有明确BD是平行四边形的边还是对角线,所以一定要分类讨论,以免漏解.

练习册系列答案
相关题目
 如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.
如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D. 如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2,与y轴交于点C(0,-4),其中x1,x2是方程x2-4x-12=0的两个根.
如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2,与y轴交于点C(0,-4),其中x1,x2是方程x2-4x-12=0的两个根. (2012•历下区一模)如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于C(0,3),M是抛物线对称轴上的任意一点,则△AMC的周长最小值是
(2012•历下区一模)如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于C(0,3),M是抛物线对称轴上的任意一点,则△AMC的周长最小值是 如图,抛物线与y轴交于点A(0,4),与x轴交于B、C两点.其中OB、OC是方程的x2-10x+16=0两根,且OB<OC.
如图,抛物线与y轴交于点A(0,4),与x轴交于B、C两点.其中OB、OC是方程的x2-10x+16=0两根,且OB<OC. 如图,抛物线与x轴交于A、B(6,0)两点,且对称轴为直线x=2,与y轴交于点C(0,-4).
如图,抛物线与x轴交于A、B(6,0)两点,且对称轴为直线x=2,与y轴交于点C(0,-4).