题目内容
 如图,抛物线与x轴交于A、B(6,0)两点,且对称轴为直线x=2,与y轴交于点C(0,-4).
如图,抛物线与x轴交于A、B(6,0)两点,且对称轴为直线x=2,与y轴交于点C(0,-4).(1)求抛物线的解析式;
(2)点M是抛物线对称轴上的一个动点,连接MA、MC,当△MAC的周长最小时,求点M的坐标;
(3)点D(4,k)在(1)中抛物线上,点E为抛物线上一动点,在x轴上是否存在点F,使以A、D、E、F为顶点的四边形是平行四边形,如果存在,直接写出所有满足条件的点F的坐标,若不存在,请说明理由.
分析:(1)首先根据抛物线与x轴交于A、B(6,0)两点,且对称轴为直线x=2可以求出A的坐标,然后设所求抛物线的解析式为y=a(x+2)(x-6),接着把C的坐标代入其中即可求解;
(2)根据题意知道当△MAC的周长最小时,即MA+MC的值最小,然后连BC,交直线x=2于点M,即为所求的点.根据作图可以求出直线BC的解析式,把x=2代入其中求出y即可解决问题;
(3)存在.首先根据已知条件求出D的坐标,然后讨论:
如图(1),当AF2为平行四边形的边时,接着根据平行四边形的性质得到E的坐标;
如图(2),当AF为平行四边形的对角线时,设E′的坐标为(x,4),把E′(x,4)代入y=
x2-
x-4得x=2±2
,由此即可求解.
(2)根据题意知道当△MAC的周长最小时,即MA+MC的值最小,然后连BC,交直线x=2于点M,即为所求的点.根据作图可以求出直线BC的解析式,把x=2代入其中求出y即可解决问题;
(3)存在.首先根据已知条件求出D的坐标,然后讨论:
如图(1),当AF2为平行四边形的边时,接着根据平行四边形的性质得到E的坐标;
如图(2),当AF为平行四边形的对角线时,设E′的坐标为(x,4),把E′(x,4)代入y=
| 1 |
| 3 |
| 4 |
| 3 |
| 7 |
解答: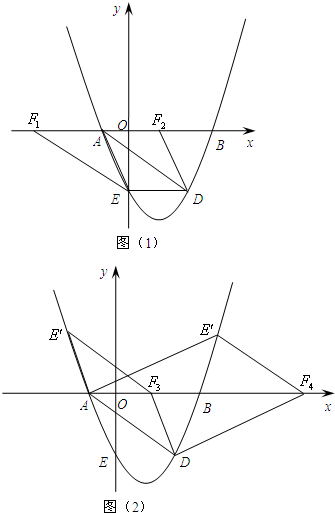 解:(1)∵抛物线与x轴交于A、B(6,0)两点,且对称轴为直线x=2,
解:(1)∵抛物线与x轴交于A、B(6,0)两点,且对称轴为直线x=2,
∴A(-2,0),
又∵抛物线过点A、B、C,
故设抛物线的解析式为y=a(x+2)(x-6),
将点C的坐标代入,
求得a=
,
∴抛物线的解析式为y=
x2-
x-4;
(2)当△MAC的周长最小时,即MA+MC的值最小,
连接BC,交直线x=2于点M,即为所求的点;
∵直线BC经过B(6,0),C(0,-4),
∴直线CB的解析式为yBC=
x-4,
当x=2时,y=-
∴M(2,-
);
(3)∵点D(4,k)在抛物线y=
x2-
x-4上,
∴当x=4时,k=-4,
∴点D的坐标是(4,-4),
如图(1),当AF2为平行四边形的边时,
∵D(4,-4),
 ∴DE=4.
∴DE=4.
∴F1(-6,0);
如图(2),当AF为平行四边形的对角线时,
F的坐标为(x,0)
把F(x,0)代入y=
x2-
x-4,
得x=2±2
.
∴F2(2+2
,0),F3(2-2
,0).
 解:(1)∵抛物线与x轴交于A、B(6,0)两点,且对称轴为直线x=2,
解:(1)∵抛物线与x轴交于A、B(6,0)两点,且对称轴为直线x=2,∴A(-2,0),
又∵抛物线过点A、B、C,
故设抛物线的解析式为y=a(x+2)(x-6),
将点C的坐标代入,
求得a=
| 1 |
| 3 |
∴抛物线的解析式为y=
| 1 |
| 3 |
| 4 |
| 3 |
(2)当△MAC的周长最小时,即MA+MC的值最小,
连接BC,交直线x=2于点M,即为所求的点;
∵直线BC经过B(6,0),C(0,-4),
∴直线CB的解析式为yBC=
| 2 |
| 3 |
当x=2时,y=-
| 8 |
| 3 |
∴M(2,-
| 8 |
| 3 |
(3)∵点D(4,k)在抛物线y=
| 1 |
| 3 |
| 4 |
| 3 |
∴当x=4时,k=-4,
∴点D的坐标是(4,-4),
如图(1),当AF2为平行四边形的边时,
∵D(4,-4),
 ∴DE=4.
∴DE=4.∴F1(-6,0);
如图(2),当AF为平行四边形的对角线时,
F的坐标为(x,0)
把F(x,0)代入y=
| 1 |
| 3 |
| 4 |
| 3 |
得x=2±2
| 7 |
∴F2(2+2
| 7 |
| 7 |
点评:此题是二次函数的综合题,分别考查了待定系数法确定函数的解析式、平行四边形的性质及轴对称的性质,综合性比较强,要求学生有很强的综合分析问题,解决问题的能力,同时相关的基础知识也熟练掌握.

练习册系列答案
相关题目
 如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.
如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D. 如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2,与y轴交于点C(0,-4),其中x1,x2是方程x2-4x-12=0的两个根.
如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2,与y轴交于点C(0,-4),其中x1,x2是方程x2-4x-12=0的两个根. (2012•历下区一模)如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于C(0,3),M是抛物线对称轴上的任意一点,则△AMC的周长最小值是
(2012•历下区一模)如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于C(0,3),M是抛物线对称轴上的任意一点,则△AMC的周长最小值是 如图,抛物线与y轴交于点A(0,4),与x轴交于B、C两点.其中OB、OC是方程的x2-10x+16=0两根,且OB<OC.
如图,抛物线与y轴交于点A(0,4),与x轴交于B、C两点.其中OB、OC是方程的x2-10x+16=0两根,且OB<OC.