题目内容
 (2012•历下区一模)如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于C(0,3),M是抛物线对称轴上的任意一点,则△AMC的周长最小值是
(2012•历下区一模)如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于C(0,3),M是抛物线对称轴上的任意一点,则△AMC的周长最小值是| 10 |
| 10 |
分析:连接BC,与抛物线的对称轴交于M,连接AM,AC,由A与B关于抛物线对称轴对称,利用两点之间线段最短得到此时△AMC的周长最小,其值等于AC+AM+CM,再由线段垂直平分线定理得到MA=MB,等量代换可得出周长最小值为AC+BC,由A、B、C三点的坐标得到OA、OB、OC的长,在直角三角形AOC与直角三角形BOC中,利用勾股定理分别求出AC与BC的长,即可得到三角形AMC周长的最小值.
解答: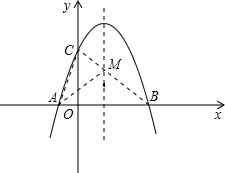 解:连接BC,与抛物线的对称轴交于M,连接AM,AC,此时△AMC的周长最小,
解:连接BC,与抛物线的对称轴交于M,连接AM,AC,此时△AMC的周长最小,
∵A(-1,0),B(4,0),C(0,3),
∴OA=1,OB=4,OC=3,
在Rt△AOC中,根据勾股定理得:AC=
=
,
在Rt△BOC中,根据勾股定理得:BC=
=5,
∵A与B关于抛物线对称轴对称,
∴MA=MB,
则△ACM周长最小值为AC+CM+AM=AC+CM+MB=AC+BC=
+5.
故答案为:
+5
 解:连接BC,与抛物线的对称轴交于M,连接AM,AC,此时△AMC的周长最小,
解:连接BC,与抛物线的对称轴交于M,连接AM,AC,此时△AMC的周长最小,∵A(-1,0),B(4,0),C(0,3),
∴OA=1,OB=4,OC=3,
在Rt△AOC中,根据勾股定理得:AC=
| OA2+OC2 |
| 10 |
在Rt△BOC中,根据勾股定理得:BC=
| OB2+OC2 |
∵A与B关于抛物线对称轴对称,
∴MA=MB,
则△ACM周长最小值为AC+CM+AM=AC+CM+MB=AC+BC=
| 10 |
故答案为:
| 10 |
点评:此题考查了抛物线与x轴的交点,以及轴对称-最短路线问题,根据题意得出周长最小值为AC+BC是解本题的关键.

练习册系列答案
相关题目
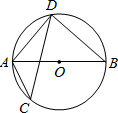 (2012•历下区一模)如图,⊙O的弦CD与直径AB相交,若∠BAD=50°,则∠ACD的度数是( )
(2012•历下区一模)如图,⊙O的弦CD与直径AB相交,若∠BAD=50°,则∠ACD的度数是( )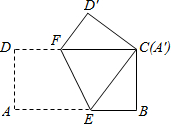 (2012•历下区一模)如图,将矩形纸片ABCD折叠,使点A与C重合,若∠CEB=45°,则∠CFE=
(2012•历下区一模)如图,将矩形纸片ABCD折叠,使点A与C重合,若∠CEB=45°,则∠CFE=