题目内容
【题目】已知:△ABC中,∠ACB=90°,AC=BC.
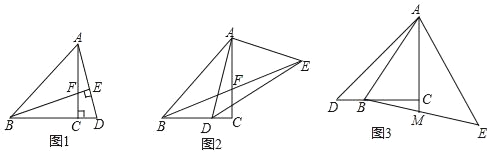
(1)如图1,点D在BC的延长线上,连AD,过B作BE⊥AD于E,交AC于点F.求证:AD=BF;
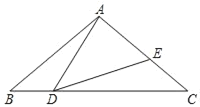
(2)如图2,点D在线段BC上,连AD,过A作AE⊥AD,且AE=AD,连BE交AC于F,连DE,问BD与CF有何数量关系,并加以证明;
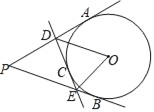
(3)如图3,点D在CB延长线上,AE=AD且AE⊥AD,连接BE、AC的延长线交BE于点M,若AC=3MC,请直接写出![]() 的值.
的值.
【答案】(1)证明见解析;(2)结论:BD=2CF.理由见解析;(3)![]() .
.
【解析】
(1)欲证明BF=AD,只要证明△BCF≌△ACD即可;
(2)结论:BD=2CF.如图2中,作EH⊥AC于H.只要证明△ACD≌△EHA,推出CD=AH,EH=AC=BC,由△EHF≌△BCF,推出CH=CF即可解决问题;
(3)利用(2)中结论即可解决问题.
(1)证明:如图1中,

∵BE⊥AD于E,
∴∠AEF=∠BCF=90°,
∵∠AFE=∠CFB,
∴∠DAC=∠CBF,
∵BC=CA,
∴△BCF≌△ACD,
∴BF=AD.
(2)结论:BD=2CF.
理由:如图2中,作EH⊥AC于H.
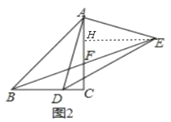
∵∠AHE=∠ACD=∠DAE=90°,
∴∠DAC+∠ADC=90°,∠DAC+∠EAH=90°,
∴∠DAC=∠AEH,
∵AD=AE,
∴△ACD≌△EHA,
∴CD=AH,EH=AC=BC,
∵CB=CA,
∴BD=CH,
∵∠EHF=∠BCF=90°,∠EFH=∠BFC,EH=BC,
∴△EHF≌△BCF,
∴FH=CF,
∴BC=CH=2CF.
(3)如图3中,同法可证BD=2CM.
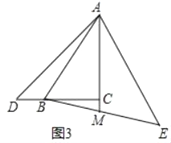
∵AC=3CM,设CM=a,则AC=CB=3a,BD=2a,
∴![]() .
.

 名校课堂系列答案
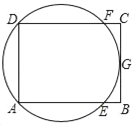
名校课堂系列答案【题目】如图,点E是矩形ABCD边AB上一动点(不与点B重合),过点E作EF⊥DE交BC于点F,连接DF.已知AB = 4cm,AD = 2cm,设A,E两点间的距离为xcm,△DEF面积为ycm2.小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.

下面是小明的探究过程,请补充完整:
(1)确定自变量x的取值范围是 ;
(2)通过取点、画图、测量、分析,得到了x与y的几组值,如下表:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | … |
y/cm2 | 4.0 | 3.7 | 3.9 | 3.8 | 3.3 | 2.0 | … |
(说明:补全表格时相关数值保留一位小数)
(3)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(4)结合画出的函数图象,解决问题:当△DEF面积最大时,AE的长度为 cm.