题目内容
【题目】问题探究:
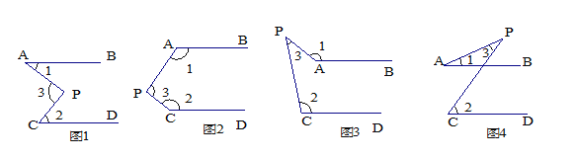
如下面四个图形中, AB∥CD.
(1)分别说出图1、图2、图3、图4中,∠1与∠2、∠3三者之间的关系.
(2)请你从中任选一个加以说明理由.
解决问题:
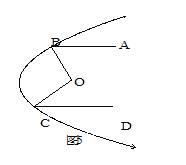
(3)如图5所示的是一探照灯灯碗的纵剖面,从位于O点的灯泡发出两束光线OB、OC经灯碗反射后平行射出.如果∠ABO=57°,∠DCO=44°,那么∠BOC=_______°.
【答案】(1) 图1:∠1+∠2=∠3; 图2:∠1+∠2+∠3=180o; 图3:∠1=∠2+∠3; 图4:∠1+∠3=∠2;(2)见解析;(3)101o
【解析】
(1) 图1:首先过点P作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,同旁内角互补,即可求得答案;
图2:首先过点P作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,内错角相等,即可求得答案;
图3:由AB∥CD,根据两直线平行,同位角线相等,以及三角形外角的性质,即可求得答案;
图4:由AB∥CD,根据两直线平行,同位角线相等,以及三角形外角的性质,即可求得答案.
(2)选图1,过过点P作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,内错角相等,即可求得答案;
(3)利用图1结论进行求解.
(1)图1:∠1+∠2=∠3;
图2:∠1+∠2+∠3=180o;
图3:∠1=∠2+∠3;
图4:∠1+∠3=∠2;
(2)选择图1,
如图所示:过点P作EP//AB,

∵AB//CD,EP//AB,
∴AB//EP//CD,
∴∠1=∠APE,∠2=∠EPC,
又∵∠3=∠APE+∠EPC,
∴∠1+∠2=∠3;
(3)由图1可得:∠BOC=∠ABO+∠DCO,
又∵∠ABO=57°,∠DCO=44°,
∴∠BOC=57°+44°=101o.






