Question

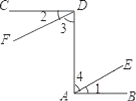
【题目】如图，将Rt△ABC绕直角顶点A逆时针旋转90°得到△ADE，BC的延长线交DE于F，连接BD，若BC＝2EF，试证明△BED是等腰三角形．

Answer 1

【答案】见解析

【解析】

根据直角三角形的两锐角互余，以及对顶角相等，旋转的性质，即可证得是的垂直平分线，据此即可证得.

证明：∵将Rt△ABC绕直角顶点A逆时针旋转90°得到△ADE，

∴DE＝BC，∠ADF＝∠ABC，

∵BC＝2EF，

∴DF＝EF，

∴DE＝2EF，

∵在直角△ABC中，∠ABC+∠ACB＝90°，

又∵∠ABC＝∠ADE，

∴∠ACB+∠ADE＝90°．

∵∠FCD＝∠ACB，

∴∠FCD+∠ADE＝90°，

∴∠CFD＝90°，

∴BF⊥DE，

∵EF＝FD，

∴BF垂直平分DE，

∴BD＝BE，

∴△BDE是等腰三角形．